I. MỞ ĐẦU
Nghiên cứu
đứt gãy trên cơ sở tài liệu trọng lực và tài liệu từ đã được các nhà địa vật lý
trong nước sử dụng khá rộng rãi [2-7, 9-10]. Các kết quả nghiên cứu trong những
năm gần đây đã chứng tỏ hướng nghiên cứu này là có hiệu quả và đã góp phần làm
sáng tỏ bức tranh về kiến tạo đứt gãy lãnh thổ Việt Nam. Phát hiện đứt gãy và
đánh giá hướng cắm, độ sâu xuất phát cũng như độ sâu kết thúc của đứt gãy là
những đối tượng được các tác giả quan tâm giải quyết. Về mặt phương pháp luận
phân tích tài liệu trọng lực thì Cao Đình Triều (2, 4, 7) đã đưa ra được một tổ
hợp phương pháp phân tích định tính và định lượng trong nghiên cứu cấu trúc đứt
gãy. Tuy vậy các phương pháp này cũng chỉ dừng ở mức phát hiện vị trí, phương
phát triển, hướng cắm của đứt gãy mà thôi. Một trong những nhiệm vụ quan trọng
là nghiên cứu bề rộng của đới phá huỷ thì các phương pháp phân tích trước đây
chưa giải quyết được. Trong khi đó việc nghiên cứu cấu trúc đới dập vỡ kiến tạo
lại có ý nghĩa lớn trong đánh giá bề rộng vùng nguồn phát sinh động đất và trong
thăm dò các loại khoáng sản khác nhau, đặc biệt là thăm dò nước và dầu khí.
Với mục
đích nâng cao hiệu quả của phương pháp phân tích trọng lực, trong khuôn khổ bài
báo này, chúng tôi bước đầu đưa ra một phương pháp phân tích tài liệu trọng lực
khu vực kết hợp với tài liệu vi trọng lực nhằm nghiên cứu bề rộng đới đứt gãy.
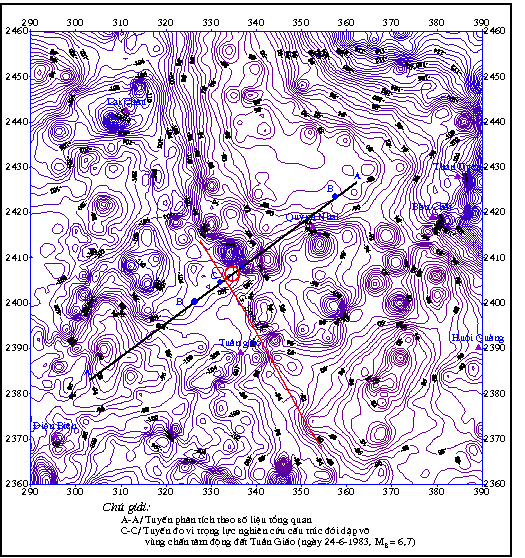
Bước đầu phương pháp này được áp dụng trong nghiên cứu đới dập vỡ vùng chấn tâm
động đất Tuần Giáo năm 1983 (Ms = 6,7).
Tài liệu chủ yếu được sử dụng trong công
trình này bao gồm:
1/ Bản đồ dị thường trọng lực vùng Tuần
Giáo tỷ lệ 1:200.000.
2/ Tuyến đo vi trọng lực cắt qua vùng chấn
tâm tỷ lệ 1:25.000 (lưu trữ tại Viện Vật lý địa cầu).
II.
TỔ HỢP PHƯƠNG PHÁP PHÂN TÍCH TÀI LIỆU TRONG NGHIÊN CỨU ĐẶC TRƯNG CẤU TRÚC ĐỚI
ĐỨT GÃY
Thông thường, nhằm mục
đích nhận dạng đặc trưng cấu trúc một đứt gãy nào đó chúng tôi sử dụng 3 phương
pháp phân tích tài liệu trọng lực Bouguer theo tuyến như [1-10]:
- Mặt cắt
građien ngang trường trọng lực theo độ sâu;
- Mặt cắt građien chuẩn hoá toàn phần; và
- Mặt cắt hệ số cấu trúc/mật độ trên cơ sở
mô hình lăng trụ tròn nằm ngang.
Các mặt cắt thành phần trường này phản ánh
khá chính xác vị trí và góc cắm của đứt gãy [2, 4, 6, 7]. Nguyên lý xây dựng hệ
phương pháp nhận dạng này là dựa trên giả thiết rằng các đứt gãy là đường cắt
chéo, chia khối cấu trúc thành các khối nhỏ, gây nên sự dịch chuyển theo phương
thẳng đứng và vì vậy đã tạo nên sự thay đổi mật độ theo chiều nằm ngang. Kết quả
phân tích dọc theo các mặt cắt nói trên chỉ là bước đầu nhằm phục vụ cho việc
thiết lập và giải bài toán ngược trọng lực để xây dựng nên mặt cắt cấu trúc đứt
gãy [2, 4, 6, 7].
Các thuật toán phân tích số liệu được lần
lượt mô tả tóm tắt như sau:
1.
Phương pháp xây dựng mặt cắt građien ngang
Građien ngang dị
thường trọng lực Bouguer được xác định trên cơ sở công thức:
![]() (1)
(1)
![]()
![]()
Građien thẳng đứng dị thường trọng lực
được xác định trên cơ sở công thức:
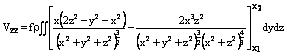 (2)
(2)
với: f - hệ số hấp dẫn trọng trường, r - giá trị mật
độ, g/cm3.
2.
Phương pháp xây dựng mặt cắt građien chuẩn hoá toàn phần
Građien chuẩn hoá toàn phần được xác định
trên cơ sở công thức:
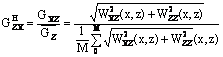 (3)
(3)
![]() - Số điểm
giá trị trọng lực Bouguer
- Số điểm
giá trị trọng lực Bouguer
![]() - Građien thẳng đứng dị thường Bouguer
- Građien thẳng đứng dị thường Bouguer
![]() - Građien nằm ngang dị thường Bouguer
- Građien nằm ngang dị thường Bouguer
3.
Phương pháp xây dựng mặt cắt hệ số cấu trúc/mật độ
Trên tuyến mặt cắt vuông góc với trục của lăng trụ tròn nằm
ngang ta có công thức xác định giá trị dị thường trọng lực như sau:
![]() (4)
(4)
R- bán kính của trụ
trong; x, z - toạ độ tâm của trụ tròn; r- giá trị mật
độ của trụ tròn; g- hệ số hấp dẫn
trọng trường (6,67 x 10-8).
Giả sử ta biết trước được giá trị građien
ngang trường dị thường trọng lực (được xác định bằng đo trực tiếp hoặc tính toán
trên cơ sở dị thường trọng lực Bouguer) Vxz gây ra bởi nhóm các lăng trụ nằm
ngang.
Trong trường hợp bài toán hai chiều, các
thông số của lăng trụ được biểu diễn trên tuyến vuông góc với lăng trụ như sau:
![]() - khoảng cách tới tâm của lăng trụ (theo trục x)
- khoảng cách tới tâm của lăng trụ (theo trục x)
![]() - độ sâu tới tâm của lăng trụ
- độ sâu tới tâm của lăng trụ
D![]() - mật độ dư của lăng trụ so với môi trường xung quanh.
- mật độ dư của lăng trụ so với môi trường xung quanh.
Khối lượng của đơn vị lăng trụ nằm ngang
được xác định bằng: ![]() . Việc xác định giá trị mật độ dư D
. Việc xác định giá trị mật độ dư D![]() và bán kính của lăng trụ (g/cm3)
và bán kính của lăng trụ (g/cm3)
![]() (km) một cách riêng
biệt là hết sức khó khăn, vì vậy ta đưa vào công thức tính dị thường trọng lực
đại lượng
(km) một cách riêng
biệt là hết sức khó khăn, vì vậy ta đưa vào công thức tính dị thường trọng lực
đại lượng ![]() sao cho:
sao cho:
![]() và phản
ánh đầy đủ dấu của mật độ dư, ta có:
và phản
ánh đầy đủ dấu của mật độ dư, ta có:
![]()
trong đó ![]()
Như vậy, mô hình trụ tròn nằm ngang được
đặc trưng bởi 4 thông số: ![]() và
và ![]() .
.
Ta thiết lập hàm:
![]() (5)
(5)
Thông số ![]() là không đổi, khi đó
mô hình trụ tròn nằm ngang được biểu diễn bằng 3 đại lượng véctơ:
là không đổi, khi đó
mô hình trụ tròn nằm ngang được biểu diễn bằng 3 đại lượng véctơ:
![]()
Các đại lượng véctơ này sẽ được xác định
trên cơ sở tiệm cận tối ưu hàm (6).
Nếu ta gọi mô hình ban đầu là: ![]() , thì các bước xấp xỉ tiếp theo sẽ được xác định trên cơ sở
công thức:
, thì các bước xấp xỉ tiếp theo sẽ được xác định trên cơ sở
công thức:
![]() ,
,
![]() , (6)
, (6)
![]()
với ![]() .
.
Các giá trị đạo hàm được xác định theo
công thức:
![]() (7)
(7)
![]()
![]() (8)
(8)
Ở đây:![]()
và  (9)
(9)
![]() được xác định theo phương pháp Newton, trên cơ sở
công thức:
được xác định theo phương pháp Newton, trên cơ sở
công thức:
![]() (10)
(10)
Quá trình giải hàm (10) bằng phương pháp
xấp xỉ tối ưu ta xác định hàm F cuối cùng, từ đó xác định được toạ độ tâm của
vật thể ![]() và
và ![]() .
.
Giả sử ta biết trước được D![]() của trụ tròn nằm ngang thì dễ dàng xác định được bán kính
theo công thức sau:
của trụ tròn nằm ngang thì dễ dàng xác định được bán kính
theo công thức sau:
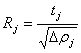 (11)
(11)
4.
Giải bài toán ngược trọng lực trên cơ sở mô hình đa giác nhiều cạnh
Trong trường hợp mô hình hai chiều với
dạng cấu trúc vật thể là đa giác n cạnh, thành phần nằm ngang và thẳng đứng dị
thường trọng lực được xác định trên cơ sở công thức:
![]() (12)
(12)
![]() (13)
(13)
trong đó: Zi và Xi là tích phân đường dọc theo cạnh thứ i
của đa giác; G- hệ số hấp dẫn trọng trường; r- mật độ của đa giác.
Trong hệ toạ độ vuông góc, nếu xác định
được toạ độ của điểm thứ i (Xi,Zi)
theo góc quay qi và bán kính ri
ta có thể xác định được Z và X theo công thức:
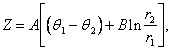 (14)
(14)
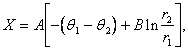 (15)
(15)
với:![]()
![]() ,
,![]()
![]() và
và ![]() .
.
Để xác định q1 và q2 ta sử dụng công
thức:
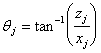 đối với j = 1,2. (16)
đối với j = 1,2. (16)
Ta biết rằng góc q1 và q2 biến đổi trong
giới hạn từ -p đến +p,
vì vậy trong khi xác định (q1-q2) sẽ xảy ra các
trường hợp sau:
1) z1 và z2 đối xứng
thì:
- khi x1z2
< x2z1 và z2 ³ 0 thì q1= q1+2p;
- khi x1z2
> x2z1 và z1 ³ 0 thì q2 = q2+2p;
- khi x1z2
= x2z1 thì X = Z = 0.
2) Nếu x1 = z1 = 0
hoặc x2 = z2 = 0 thì X = Z = 0, và
3) Nếu x1 = x2,
thì ![]()
![]()
III.
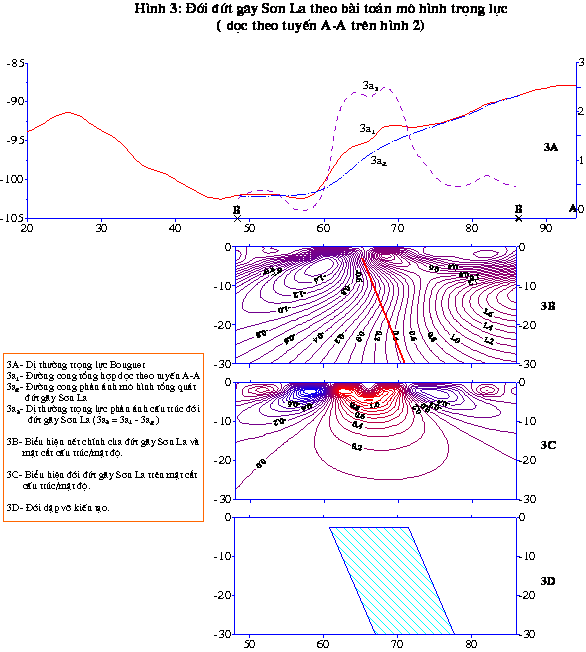
NGHIÊN CỨU BỀ RỘNG ĐỚI ĐỨT GÃY SƠN LA TẠI VÙNG CHẤN TÂM ĐỘNG ĐẤT TUẦN GIÁO TRÊN
CƠ SỞ TÀI LIỆU TRỌNG LỰC
Trên thực tế, trong quá trình vận động
kiến tạo, tác động của lực xiết ép đã tạo ra đới cà nát biến dạng với bề rộng
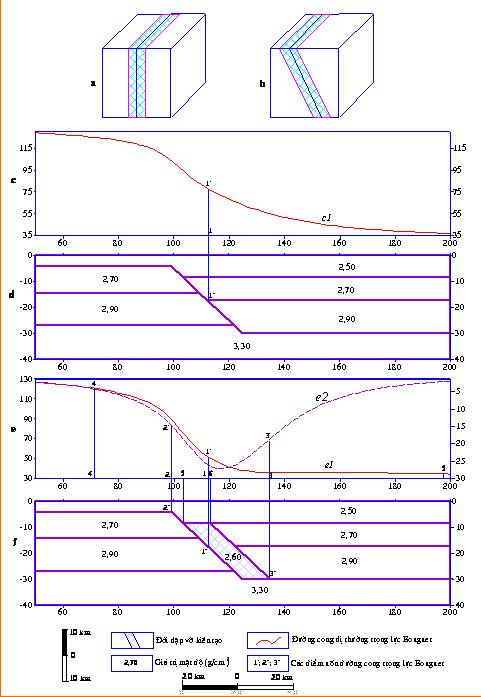
lớn mà có nơi có thể đạt tới hàng chục km (Hình 1a,1b). Như vậy việc xem xét mô
hình phân tích bỏ qua đới cà nát, dập vỡ kiến tạo trong nghiên cứu trọng lực chi
tiết là chưa đầy đủ. Để minh chứng cho việc thiết lập tổ hợp phương pháp nghiên
cứu, chúng tôi đưa ra bài toán thuận trọng lực theo mô hình phân tích được biểu
diễn trong hình 1c, 1d, 1e và 1f. Nếu ta quan niệm đứt gãy là một đường cắt
chéo, tạo một góc 45o, và gây nên sự thay đổi các mặt ranh giới cấu
trúc như trong hình 1d thì trường trọng lực Bouguer tính toán được có dạng như
trong hình c1. Bây giờ ta xem đứt gãy là một đới cà nát, biến dạng như mô hình
cấu trúc được biểu diễn trong 1f. Kết quả tính toán dị thường trọng lực Bouguer
theo mô hình 1f được đặc trưng bằng đường cong e1 trong hình 1e. Nếu ta lấy giá
trị đường cong trọng lực e1 (Hình 1e) trừ đi giá trị trọng lực tương ứng c1
(Hình 1c), ta nhận được đường cong e2 (Hình 1e) là thành phần trường trọng lực
Bouguer phản ánh đới dập vỡ kiến tạo. Trên cơ sở phân tích theo các phương pháp
truyền thống [1-4, 6-9] ta có thể xác định được bề rộng đới đứt gãy là đoạn
chiều dài điểm 5 đến điểm 6, bề rộng ảnh hưởng của đới đứt gãy là đoạn chiều dài
từ điểm 2 đến điểm 3 trong hình 1f. Như vậy, đới dập vỡ của đứt gãy có thể xác
định được trên cơ sở phân tích tài liệu trọng lực. Trong trường hợp đới đứt gãy
lớn đi kèm nhiều đứt gãy thứ cấp thì theo nguyên lý phân tích tương tự, với tài
liệu chi tiết hơn chúng ta cũng có thể xác định được. Đây là cơ sở lý thuyết cơ
bản trong nghiên cứu cấu trúc đới đứt gãy theo tài liệu trọng lực.
Như vậy,
để nghiên cứu bề rộng đới đứt gãy chúng ta tiến hành các bước phân tích sau đây:
1. Xác định hướng cắm và góc cắm cũng như
độ sâu ảnh hưởng của mặt đứt gãy theo tài liệu trọng lực khu vực trên cơ sở cho
rằng đứt gãy là một mặt phẳng.
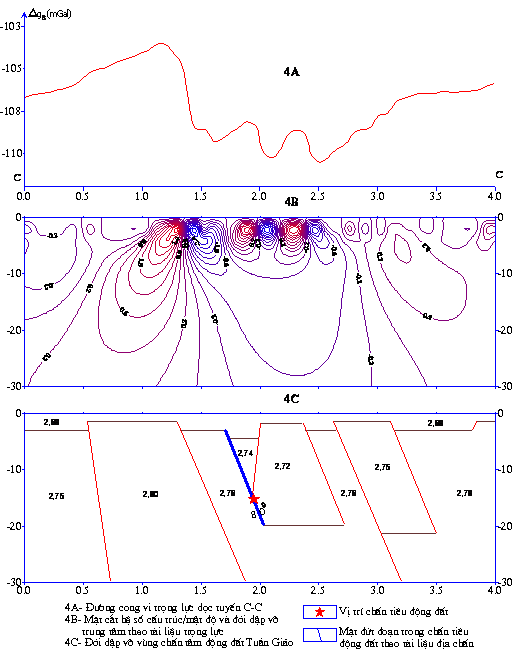
2. Nghiên
cứu cấu trúc đới đứt gãy trên cơ sở tài liệu trọng lực chi tiết (hoặc tài liệu
vi trọng lực đối với các đới đứt gãy nhỏ).