THỬ NGHIỆM PHÂN VÙNG VÀ DỰ BÁO CÁC ĐẶC TRƯNG CHUYỂN DỊCH HIỆN ĐẠI VỎ TRÁI
ĐẤT KHU VỰC TÂY BẮC BỘ TRÊN CƠ SỞ NGHIÊN CỨU MỐI TƯƠNG TÁC GIỮA TRƯỜNG ỨNG SUẤT KHU VỰC VỚI MỘT SỐ HỆ
THỐNG ĐỨT GÃY
NGUYỄN VĂN VƯỢNG1, VŨ VĂN TÍCH1,
NGUYỄN NGỌC THỦY2, BÙI VĂN DUẨN2
1Trường Đại học KHTN Hà Nội, Nguyễn Trãi,
Thanh Xuân, Hà Nội
2Viện Vật lý Địa cầu, Viện KH&CN VN, Hoàng Quốc Việt, Cầu Giấy, Hà
Nội
Tóm tắt: Sự xác định bản chất của biến dạng nội mảng và
chuyển dịch hiện đại có thể xảy ra dọc các hệ đứt gãy chính dưới tác động của
trường ứng suất khu vực đóng vai trò cực kỳ quan trọng trong việc phân vùng và
dự báo động đất cũng như các tai biến tự nhiên liên quan. Một cách tiệm cận mới
được phát triển trong lĩnh vực kiến tạo vật lý đã được áp dụng để nghiên cứu
hoạt động đứt gãy trong giai đoạn hiện đại khu vực Tây Bắc Bộ. Cách tiệm cận này
dựa trên cơ sở đánh giá và tính toán mối quan hệ giữa ứng suất khu vực với các
thông số mô tả hành vi, động hình học của các đoạn đứt gãy khu vực nghiên cứu.
Kết quả tính toán đã cho phép xác lập được các đặc trưng về sự biến đổi ứng suất
trong không gian và sự chuyển dịch tương đối của các yếu tố cấu trúc trong toàn
bộ vùng nghiên cứu. Cơ cấu chấn tiêu cũng được dự báo cho một số điểm dọc theo
một số đứt gãy chính trong khu vực.
Kết quả nghiên cứu cho thấy có thể áp dụng cách tiệm cận này để giải
quyết bài toán phân vùng chi tiết và dự báo các tai biến địa động lực như động
đất, nứt đất ở Việt Nam.
I. CÁCH TIỆM CẬN
Hiện nay có nhiều
cách tiệm cận trong việc phân vùng và dự báo chi tiết động đất. Ví dụ phân vùng
và dự báo trên cơ sở gia tốc dao động nền, trên cơ sở chấn cấp dự báo cực đại,
dự báo trên cơ sở quan trắc sự biến thiên nồng độ khí rađon, CO2 ,
ion Ca++, Hg,... sự biến thiên tính chất điện, từ telur [5, 7]. Một
trong các hướng nghiên cứu đang được tiến hành ở các nước hay xảy ra động đất
như Mỹ, Nhật, Pháp, New Zealand, Thổ Nhĩ Kỳ... là hướng nghiên cứu về sự tiến
triển và biến đổi của trạng thái ứng suất dọc theo các đới đứt gãy. Các kết quả
nghiên cứu đó cho thấy mối quan hệ chặt chẽ giữa việc gia tăng ứng suất với sự
xuất hiện động đất. Động đất thường xuất hiện ngay sau khi ứng suất lệch tại một
khu vực nào đó dọc đới đứt gãy vượt quá một giới hạn nào đó. Hiện tượng này đã
quan sát thấy ở đới đứt gãy San Andreas vào các năm 1975, 1979, 1986, 1992, 1999
và nhiều đứt gãy sinh chấn khác trên thế giới.
Sự gia tăng ứng suất phụ thuộc vào mối quan hệ giữa tác động của trường
ứng suất khu vực (sinh ra do sự tương tác của các mảng kiến tạo, hoặc thay đổi
trạng thái và chế độ địa nhiệt trong vỏ) với các đặc trưng hình động học của các
hệ đứt gãy trong phạm vi lãnh thổ nghiên cứu. Chính vì vậy, việc nghiên cứu đặc
điểm và bản chất của các quá trình biến dạng nội khối cũng như các đặc trưng
chuyển động hiện đại dọc theo các đứt gãy dưới tác động của trường ứng suất khu
vực đóng vai trò cực kỳ quan trọng đối với công tác nghiên cứu phân vùng và dự
báo chi tiết động đất cũng như các tai biến liên quan.
Trong bài báo này,
chúng tôi trình bày một mô hình thử nghiệm việc nghiên cứu, đánh giá mối quan hệ
giữa trường ứng suất khu vực với các thông số mô tả trạng thái và hành vi của 15
đoạn đứt gãy ở Tây Bắc Bộ, phục vụ cho việc nghiên cứu phân vùng và dự báo các
tai biến liên quan.
II. PHƯƠNG PHÁP
NGHIÊN CỨU
1. Nghiên cứu thực địa
Trong lịch sử phát
triển địa chất khu vực, các hệ thống đứt gãy ở Tây Bắc Bộ nói riêng, cũng như ở
Việt Nam nói chung, đã trải qua nhiều lần tái hoạt động, nên dấu ấn của các hoạt
động mà ta quan sát thấy trên bình đồ cấu trúc hiện nay thường là sản phẩm tổng
hợp của nhiều giai đoạn. Chính vì vậy, việc xác định rõ các đặc trưng động học
của chuyển dịch đương đại để làm cơ sở cho việc tính toán dự báo các trường dịch
chuyển dọc theo các đứt gãy đóng vai trò cực kỳ quan trọng. Trong nghiên cứu
thực địa, việc đầu tiên cần làm là tiến hành tách các biểu hiện của chuyển động
đương đại dọc theo một đứt gãy bất kỳ ra khỏi các dấu ấn biến dạng của các giai
đoạn kiến tạo cổ hơn, để từ đó xác định được chính xác đặc trưng chuyển động
hiện đại của đứt gãy.
Để có số liệu cho việc nghiên cứu thử nghiệm này, chúng tôi
đã tiến hành tách các pha hoạt động kiến tạo trên cơ sở nghiên cứu kết hợp giữa
các biểu hiện địa mạo của đứt gãy, đặc điểm địa hình ở hai cánh của đứt gãy, đặc
điểm biến dạng dẻo giòn của các đá quan sát dọc theo đứt gãy trên thực địa, theo
các phương pháp được mô tả trong tài liệu [3, 5, 10]. Việc tính toán trạng thái ứng suất và tách pha kiến tạo được thực
hiện chủ yếu theo phương pháp của Angelier [1] và các phương pháp trình bày
trong [2, 6, 8].
2. Các thông số của trường ứng suất khu vực
Các thông số về trạng thái ứng
suất khu vực được sử dụng để tính toán và dự báo dựa trên hai nguồn tài liệu
chính. Nguồn thứ nhất dựa vào bản đồ và báo cáo của chương trình nghiên cứu về
“ứng suất thạch quyển thế giới” do GS. Zoback chủ trì hoàn thành năm 1992 [11].
Các kết quả của chương trình này cũng trùng với kết quả tính toán trường tốc độ
dịch chuyển của khu vực nằm kẹp giữa đứt gãy Sagaing (Myanmar) và đứt gãy Sông
Hồng trong đó có khu vực Tây Bắc Bộ trên cơ sở số liệu của các trận động đất thu
được trong vòng 85 năm [4].
Nguồn tài liệu thứ hai dựa trên các kết quả xác định trạng
thái ứng suất tác động tới khu vực nghiên cứu từ Pliocen - Đệ tứ trở lại đây của
các tác giả bài báo này. Các kết quả xác định trạng thái ứng suất trên thực địa
được đối chiếu với các thông số ứng suất khu vực và được sử dụng như một nguồn
thông tin nhằm xác định tỷ lệ tương đối của 3 trục ứng suất chính.
3. Phương pháp tính toán
Cơ sở lý thuyết của quá trình tính toán các đặc trưng dịch
chuyển và sự biến động của các thông số ứng suất dưới tác động tổng hợp của ứng
suất khu vực và hành vi của các đứt gãy gây ra được mô tả chi tiết trong tài
liệu công bố của Okada [9]. Các tham số dịch trượt và đạo hàm của chúng theo các
hướng đông, bắc và thẳng đứng được tính toán trong môi trường bán không gian
đồng nhất. Biến dạng sẽ được chuyển thành các giá trị ứng suất thông qua định
luật Hooke tổng quát sử dụng mođul độ cứng là 2,68x1010
Nm-2. Các giá trị ứng suất có thể quay và chuyển đổi sang hệ toạ độ
bất kỳ để tính toán cho các đứt gãy có định hướng tuỳ ý sử dụng phép chuyển vị
tensor bậc hai.
4. Tham số chính được đưa vào tính toán
Các tham số động
hình học của các đứt gãy hoặc đoạn đứt gãy được đưa vào sử dụng trong thử nghiệm
phân vùng và dự báo các chuyển dịch đương đại được cho trong bảng 1.
Hệ số ma sát tĩnh
được sử dụng trong tính toán là 0,65, hệ số áp lực lỗ rỗng là 0,38, hệ số
Skempton (hệ số tính đến sự thay đổi áp suất lỗ hổng do sự nén ép) là 0,5. Hệ số
ứng suất là R = 0,02 và R = 0,95 (R = (S2-S3)/(S1-S3)).
Các giá trị bằng số của S1 = -500 bar, S2
= 0 và -450 bar, S3= 10 và 500 bar được tính cho hai trường hợp tương
ứng với R = 0,02 và 0,95. Định hướng của trường ứng suất khu vực S1:
340/25; S3: 080/20,45. Bề dày lớp vỏ giòn là 15 km. Kích thước ước tính là 3x3
km. Đối với đứt gãy mà mức độ hoạt động trong tương lai chưa rõ thì chấn cấp
được lấy bằng Mw = 0. Trong trường hợp đó, đứt gãy được coi như một
đường nứt.
Bảng 1. Các tham số động hình học của các
đứt gãy được sử dụng để tính toán
Tên đứt gãy
|
Dài (km)
|
Rộng
(km)
|
Phương
|
Góc dốc
|
Góc trượt
|
Chế độ kiến tạo
|
Mw max
|
|
Đoạn tây bắc Sông Đà
|
130
|
15
|
330
|
80
|
-165.25
|
PT
|
6
|
|
Đoạn Mường La - Bắc Yên
|
88
|
15
|
300
|
80
|
-165.96
|
P
|
6
|
|
Đoạn Bắc Yên - Gia Phù
|
33
|
15
|
322
|
80
|
-146
|
P
|
6
|
|
Đứt gãy Điện Biên Phủ
|
150
|
20
|
017
|
80
|
-36.86
|
T-TT
|
6,8
|
|
Phong Thổ - Than Uyên
|
87
|
15
|
138
|
75
|
-131.2
|
TP
|
4
|
|
Đoạn bắc Tủa Chùa
|
110
|
15
|
170
|
90
|
-145
|
TP
|
6,8
|
|
Đoạn Nam Tuần Giáo
|
60
|
15
|
140
|
80
|
-141
|
PT
|
6,8
|
|
Thuận
Châu - Sơn La
|
144
|
12
|
315
|
80
|
-110
|
T-TP
|
6
|
|
Sông Mã: đoạn
tây bắc
|
177
|
25
|
315
|
80
|
-165
|
P
|
6
|
|
Sông Mã: đoạn trung tâm
|
84
|
25
|
290
|
80
|
-160
|
P
|
6,8
|
|
Sông Ma: đoạn đông nam
|
137
|
25
|
330
|
80
|
-160
|
P
|
6,8
|
|
Sông Hồng
|
400
|
25
|
312
|
80
|
-160
|
P
|
6
|
|
Đoạn thượng Sông Đà 1
|
83
|
10
|
125
|
90
|
-170
|
P
|
4
|
|
Đoạn thượng Sông Đà 2
|
93
|
10
|
125
|
90
|
-170
|
P
|
4
|
|
Đứt gãy Pu May Tun
|
112
|
10
|
130
|
90
|
-168.6
|
P
|
0
|
Ghi chú: T-TP =
thuận - thuận phải; PT = phải thuận; TP = thuận phải; T-TT = thuận -
thuận trái.
III. KẾT QUẢ NGHIÊN CỨU VÀ THẢO LUẬN
1. Kết quả phân vùng và dự báo các đặc trưng chuyển
dịch
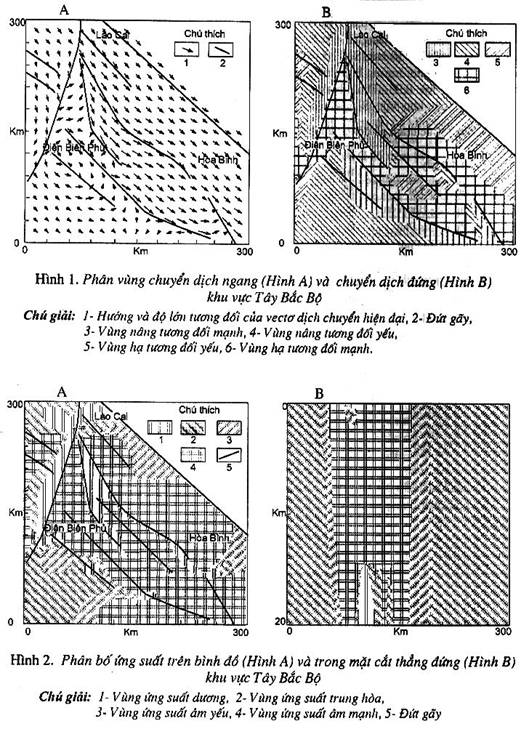
Kết quả phân vùng
dịch chuyển ngang và đứng vật chất vỏ Trái đất trong giai đoạn đương đại được
đưa ra ở hình 1 và tính cho trưòng hợp R = 0,95. Trên sơ đồ này, phổ màu và độ
lớn của vectơ cho thấy biên độ chuyển dịch tương đối của vật chất vỏ, hướng của
vectơ tương ứng với xu thế chuyển dịch của chúng. Trên hình 1 ta thấy toàn bộ
vật chất vỏ của khu vực Tây Bắc Bộ đều có xu thế chuyển dịch về phía đông nam.
Tuy nhiên tốc độ chuyển dịch tương đối giữa các miền là không đồng nhất. Miền
phổ màu đỏ có tốc độ dịch trượt lớn nhất. Nó tương ứng với khu vực nằm giữa đứt
gãy Tuần Giáo - Tủa Chùa, đứt gãy Sông Mã và đứt gãy Sông Đà. Miền phổ màu xanh
nước biển có tốc độ chuyển dịch thấp nhất. Dọc theo từng đứt gãy, chiều của
vectơ dịch trượt và độ lớn của từng vectơ thể hiện rất rõ đặc điểm hình động học
của từng đứt gãy. Ví dụ, đối với đứt gãy Điện Biên, các nghiên cứu thực địa cho
thấy biểu hiện bề mặt của đứt gãy này trong giai đoạn đương đại dịch chuyển theo
cơ chế trượt bằng trái với hợp phần thuận. Các vectơ dịch trượt nằm ở cánh treo
có xu thế chạy về hướng bắc đông bắc, trong khi đó các vectơ ở cánh nằm của đứt
gãy chạy theo hướng bắc nam. Kết quả tổng hợp của các vectơ này sẽ cho ta cơ chế
dịch trượt trái. Hợp phần dịch trượt về đông bắc sẽ tạo ra các trũng căng giãn
quan sát được ở Điện Biên, ở Mường Pồn và ở Lai Châu. Điều này hoàn toàn khớp
với tài liệu thực tế.
Để xem xét sự phụ
thuộc và xu thế dịch chuyển của của vật chất vỏ theo độ sâu, chúng tôi tiến hành
tính toán các giá trị của vectơ dịch trượt trên mặt cắt thẳng đứng có phương vị
600 và đi qua khu vực Sơn La. Kết quả tính toán cho thấy, độ lớn và
chiều của vectơ dịch trượt có sự biến thiên tương đối rộng. Điều này phản ánh
các đứt gãy trong khu vực nghiên cứu, ngoài các hợp phần trượt bằng ngang, còn
bị chi phối bởi các chuyển động đứng tương đối của hai cánh đứt gãy đối với
nhau. Kết quả tính toán này cũng phù hợp với hành vi của đứt gãy trên thực tế.
Ví dụ như ở đứt gãy Sơn La cánh phía đông bắc thể hiện sự sụt tương đối rõ ràng
so với cánh tây nam. Xu thế chuyển dịch theo chiều thẳng đứng của khu vực nghiên
cứu được thể hiện trên hình 1B. Phổ màu thể hiện mức độ nâng hạ khác nhau. Các
miền có màu đỏ sẫm là các miền nâng, còn màu xanh nước biển tương ứng với các
miền hạ tương đối. Trên hình ta thấy rõ phía tây của đứt gãy Điện Biên, dãy Su
Xung Chao Chai nằm về phía tây nam đới Sông Mã, khu vực Cao nguyên Sin Chai, Tam
Đường, Phong Thổ nằm trong miền có xu thế nâng tương đối. Còn khu vực phía nam
Mường La, Điện Biên, Mường Ảng nằm trong miền hạ tương đối.
2. Kết quả phân vùng và dự báo ứng suất
Ta biết rằng sự
phân bố ứng suất trong toàn bộ khu vực sẽ bị biến đổi do sự có mặt của các đứt
gãy với cơ chế chuyển động khác nhau trên bình đồ hiện tại. Sự tương tác của
trường ứng suất khu vực với các hệ đứt gãy sẽ quyết định giá trị các thành phần
ứng suất tại các điểm khác nhau trong miền nghiên cứu. Các miền nằm trong vùng
có màu nóng như màu đỏ, da cam... sẽ chịu tác động của ứng suất nén. Còn màu
xanh chỉ thị cho các miền nằm trong vùng chịu tác động của ứng suất giãn. Kết
quả tính toán thể hiện trên hình 2A cho thấy miền tập trung ứng suất nén nằm ở
phía tây của đứt gãy Điện Biên, miền nằm giữa đứt gãy Tuần Giáo - Tủa Chùa và
đoạn đứt gãy bắc Sông Đà, đoạn đứt gãy Bắc Yên - Phù Yên và một vài điểm ở đứt
gãy Sông Mã và ở phía nam đứt gãy Thuận Châu - Sơn La. Phần còn lại của khu vực
nghiên cứu hầu như nằm trong miền có chế độ ứng suất giãn. Điều này phù hợp với
việc xuất hiện các hệ thống khe nứt mở và nứt đất phát triển theo các phương chủ
đạo tây bắc - đông nam, á kinh tuyến và á vĩ tuyến quan sát được ở nhiều nơi
trong khu vực nghiên cứu.
Sự biến thiên ứng
suất theo độ sâu được thể hiện trên hình 2B. Ta nhận thấy ứng suất chủ đạo vẫn
là ứng suất giãn. Ứng suất nén chỉ tập trung ở độ sâu từ 0 đến 2 km và 12 đến 20
km đối với đoạn đứt gãy nam Tuần Giáo. Phần còn lại của mặt cắt thể hiện chủ yếu
trạng thái ứng suất giãn.
3. Kết quả phân vùng và dự báo cơ cấu chấn tiêu
trên mặt
Sau khi tính toán
được các thành phần của ứng suất cho từng yếu tố của lưới, có thể xác định cơ
cấu chấn tiêu dự báo cho mọi điểm bất kỳ nằm trong khu vực nghiên cứu. Các kết
quả được cho dưới dạng số thể hiện các thông số về đường phương, góc dốc mặt đứt
gãy và góc dốc đường trượt của hai “đứt gãy” chịu tác động của ứng suất cắt cực
đại. Hai “đứt gãy” được dự báo có thể trùng với hai đứt gãy tồn tại thật hoặc
hai phương xung yếu nhất sẽ hình thành và dịch chuyển khi có điều kiện thuận
lợi.
Đối với các kết
quả ứng suất được thể hiện trên bình đồ, “cơ cấu chấn tiêu” cho phép dự báo được
các hệ thống đứt gãy nào sẽ có khả năng dịch chuyển và dịch chuyển như thế nào. Hình 3 thể hiện sơ đồ phân bố ứng suất thu nhỏ và hai cơ cấu chấn
tiêu tối ưu cho một điểm bất kỳ cần dự báo. Đối với khu vực Điện Biên, các hệ
đứt gãy tây bắc - đông nam và á kinh tuyến đều có thể dịch chuyển. Tuy nhiên so
sánh hình bên trái với hình bên phải ta nhận thấy đứt gãy phương TB-ĐN ở hình
bên trái có góc dốc nhỏ hơn đứt gãy ở hình bên phải. Góc trượt cũng khác nhau.
Đối với các đứt gãy có phương á kinh tuyến thì ngược lại. Dọc theo đứt gãy
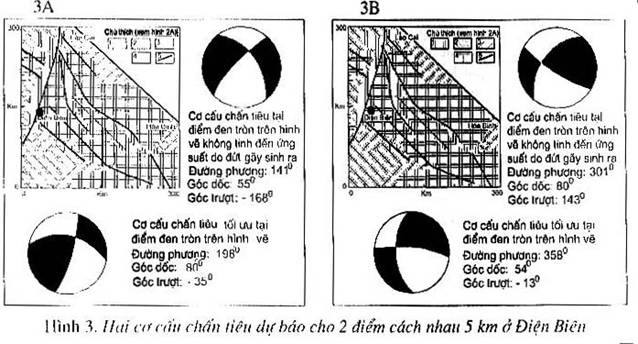
Điện Biên, cơ cấu
chấn tiêu dự báo cho vùng Mường Pồn ứng với R = 0,02 và R = 0,95 cho thấy có sự
sai khác nhỏ về góc dốc, góc trượt. Sự khác biệt này sẽ dẫn đến thành phần thuận
trong trường hợp R = 0,02, thành phần nghịch trong trường hợp R = 0,95. Sự thay
đổi này cho thấy vùng đang khảo sát tỏ ra nhạy cảm đối với sự thay đổi ứng suất.
Đối với vùng bắc
Lai Châu, cơ cấu chấn tiêu dự báo cho hai điểm nằm cách nhau khoảng 8 km khi R =
0,02 cho thấy có sự khác biệt nhỏ về hướng cắm của “đứt gãy” và góc trượt của
các đứt gãy phương tây bắc - đông nam. Đối với đứt gãy hướng á kinh tuyến, hầu
như không có sự khác biệt nào về các thông số của cơ cấu chấn tiêu. Khi tính cơ
cấu chấn tiêu dự báo với R = 0,95 cho cả hai đứt gãy hướng á kinh tuyến và tây
bắc - đông nam đều không thể hiện sự khác biệt nào.
Cơ cấu chấn tiêu
dự báo cho vùng đứt gãy Sơn La - Thuận Châu trong hai trường hợp R = 0,02 và R =
0,95 cho thấy không có sự sai khác đáng kể nào về các thông số của cơ cấu chấn
tiêu dự báo. Điều này cho thấy tại điểm khảo sát thuộc đứt gãy Sơn La - Thuận
Châu không nhạy cảm đối với sự thay đổi ứng suất. Nếu việc dự báo được tính cho
toàn bộ tuyến đứt gãy thì có thể dự báo hoạt động động đất cho đứt gãy này. Giả
sử toàn bộ các cơ cấu dự báo dọc đứt gãy đều giống như kết quả được trình bày ở
đây thì có thể nói rằng đứt gãy này ít có nguy cơ gây động đất.
Cơ cấu chấn tiêu
dự báo cho vùng Tuần Giáo: cơ cấu chấn tiêu dự báo tính được cho thấy sự thay
đổi ứng suất sẽ dẫn đến các “đứt gãy” có các phương khác nhau và góc dốc khác
nhau sẽ dịch chuyển. Tại vùng nằm ở phía bắc Tủa Chùa, trong đới đứt gãy Tuần
Giáo - Tủa Chùa, khi thay đổi trạng thái ứng suất sẽ dẫn đến cơ cấu chấn tiêu dự
báo có sự thay đổi lớn, từ nén ép gây đứt gãy nghịch cho hệ thống đông bắc - tây
nam khi R = 0,02 đến trượt bằng với góc trượt nghiêng so với phương nằm ngang 140
khi R = 0,95. Sự thay đổi như vậy cho thấy đây là vùng nhạy cảm đối với sự
thay đổi ứng suất và có thể là vùng dễ phát sinh động đất.
Nhận xét chung: Tại các vùng Điện Biên, bắc Lai Châu, nam Tuần Giáo,
bắc Tủa Chùa, cơ cấu chấn tiêu tính cho các lưới tọa độ gần nhau có sự thay đổi
lớn. Các điểm khác của khu vực Tây Bắc Bộ, cơ cấu chấn tiêu dự báo không có sự
thay đổi nhiều. Trong cả hai trường hợp tính cho R = 0,02 và R = 0,95, các thông
số khác đều giữ nguyên chỉ có hệ số ứng suất thay đổi. Vùng phía nam Tuần Giáo
đặc biệt nhạy cảm với sự biến đổi của hệ số ứng suất. Các điểm tính trong một số
trường hợp chỉ cách nhau chưa đầy 10 km, cơ cấu chấn tiêu tính được đã có sự
khác biệt lớn. Sự khác biệt này cho thấy, trong trường hợp, mặc dù không xảy ra
động đất, nhưng hầu như tất cả các hệ thống đứt gẫy có định hướng không gian
khác nhau đều có khả năng dịch chuyển dưới tác động của trường ứng suất hiện
hữu.
4. Dự báo cơ cấu chấn tiêu theo độ sâu
Để đánh giá sự
biến đổi của cơ cấu chấn tiêu theo độ sâu, chúng tôi tiến hành tính toán sự thay
đổi ứng suất tiếp cực đại trên mặt cắt đi qua vùng Sơn La và có đường phương 600 khi R = 0,95. Kết quả dự báo cho thấy ở các điểm có sự biến
đổi nhanh về giá trị ứng suất tiếp cực đại thi cơ cấu chấn tiêu tính được cũng
có sự biến đổi lớn. Từ bề mặt xuống đến độ sâu 13 km, hầu như không thấy có sự
thay đổi nào đáng kể về cơ cấu chấn tiêu. Tuy nhiên trên cả hai phương đứt gãy,
góc trượt có xu hướng tăng dần. Điều đó cho thấy hợp phần dịch chuyển thẳng đứng
cũng được tăng theo độ sâu. ở độ sâu 14 km, ta thấy rõ có sự
thay đổi đột biến về cơ cấu chấn tiêu dự báo và chuyển từ trượt bằng sang căng
giãn gần như hoàn toàn. Xuống đến độ sâu 16 km cơ cấu chấn tiêu dự báo lại trở
về trạng thái bình thường.
Như vậy, cơ cấu
chấn tiêu dự báo phụ thuộc chặt chẽ vào sự thay đổi của ứng suất tiếp cực đại.
Theo độ sâu, giá trị ứng suất cũng biến động vì vậy có thể sinh ra các cơ cấu
chấn tiêu khác nhau.
KẾT LUẬN
Các kết quả thử
nghiệm trình bày trong bài báo này cho thấy đây là một cách tiệm cận hiện đại và
có hiệu quả cao trong việc nghiên cứu phân vùng và dự báo chi tiết các đặc trưng
của địa động lực hiện đại và các tai biến liên quan như động đất, nứt đất, trượt
lở đất, đặc biệt là có thể áp dụng có hiệu quả trong công tác nghiên cứu, phân
vùng chi tiết và dự báo động đất ở Việt Nam.
Cách tiệm cận này
dựa trên cơ sở nghiên cứu, đánh giá mối quan hệ giữa trường ứng suất khu vực với
các đặc trưng hình động học của các đoạn đứt gãy trong vùng nghiên cứu. Phương
pháp này cho phép xác định sự biến thiên trạng thái ứng suất trong không gian và
dự báo các thành phần chuyển dịch theo các phương bắc nam, đông tây và thẳng
đứng của vùng nghiên cứu. Ngoài ra, phương pháp được sử dụng còn cho phép tính
toán và dự báo cơ cấu chấn tiêu cho bất kỳ điểm nào nằm trong miền nghiên cứu kể
cả dự báo theo độ sâu.
Lời
cám ơn: Các tác giả bài báo xin trân trọng cảm ơn các GS.
Angelier, Robinson và
Lepvrier đã cung cấp tư liệu và chương trình máy tính cũng như các ý kiến
trao đổi khoa học quý báu. Bài báo được hoàn thành với sự hỗ trợ kinh phí của Đề
tài nghiên cứu cơ bản mã số 713204 và Đề tài KC08-10.
VĂN LIỆU
1.
Angelier J., Tarantola A., Valette B., Manoussis S., 1982. Inversion of field data in fault tectonics to obtain
the regional stress. 1. Single phase fault populations: a new method of
computing the stress tensor. Geophysical
J. of the Royal Astr. Soc. 69 : 607–621.
2.
Fry N., 1999. Striated faults: visual
appreciation of their constraint on possible paleostress tensors. J. of
Structural Geology, 21 : 7–21. 202.
3. Gudmundsson A., S. S. Berg, K. B. Lyslo, E.
Skurtveit, 2001. Fracture networks and fluid transport
in active fault zones. J. of Structural
Geology, 23 : 343-353.
4. Holt W. E., Ni J. F., Wallace T. C., Haines A. J.,
1991. The active tectonics of the Eastern Himalayan
syntaxis and surrounding regions. J. of
Geophysical research, 96/B9 : 14595-14632.
5.
Keller
E. A., Pinter N., 1996.
Active tectonics: Earthquake, Uplift and landscape. Prentice Hall. 338p.
6. Lisle R. J., Vandycke S., 1996. Separation of multiple stress events by fault
striation analysis: an example from Variscan and younger structures at Ogmore, South
Wales. J. of the Geol.
Society, 153 : 945–953. London.
7.
Madden T. R.,
Randal L. M.,
1996. What electrical measurements can
say about changes in fault systems. In:
“Earthquake prediction: The scientific Challenge” Proc. of Colloquium. NAS, in
Ivrine,
CA.
8.
Morewooda
N. C.,
G.
P. Robertsb,
2001. Comparison of surface slip and
focal mechanism slip data along normal faults: an example from the eastern
Gulf
of Corinth, Greece.
J. of Structural Geology, 23 : 473-487.
9.
Okada
Y., 1992. Internal deformation due to shear and tensile faults in half-space. Bull. of the Seism. Soc. of America, 82/ 2 : 1018-1040.
10.
Shum
S. A., Dumont
J. E.,
Holbrook J.
M.,
2000. Active tectonics and alluvial rivers. Cambridge University
Press. 276p.
11.
Zoback
M. L., 1992.
First and second-order pattern of stress in the lithosphere: the world stress
map project. J. of Geophysics research,
97 : 11703-11728.

