2.1. Các phương pháp định tuổi dựa trên nguyên tắc thiết lập đường đẳng thời (Rb-Sr, Sm-Nd, Re-Os)

Ba phương pháp xác định tuổi đồng vị Rb-Sr, Sm-Nd và Re-Os đều dựa trên nguyên tắc xây dựng đường đẳng thời (isochron). Để hiểu một cách khái quát, chúng ta trở lại phương trình (5.6)

D = D₀ + N (e ^-lt - 1)

Việc xác định số lượng tuyệt đối của các đồng vị gặp rất nhiều khó khăn, nên thường thay thế bằng xác định tỉ lệ các đồng vị. Trong quá trình phân rã phóng xạ, đồng vị bền nào đó (S), mà hàm lượng của nó trong đá (hay khoáng vật) không bị thay đổi theo thời gian, được chọn để chuẩn hoá vế trái và vế phải của phương trình (5.6).

(D/S)_m = (D₀/S)₀ + (N/S)_m´ (e ^-lt - 1) (5.9)

ở đây các kí hiệu "m" và "0" tương ứng các tỉ lệ đo tại thời điểm t và lúc hình thành hệ (tỉ lệ ban đầu). Phương trình (5.9) tương tự phương trình đồng quy tuyến tính kiểu: y = a + bx. Do đó, nếu xem hệ các khoáng vật cùng một tuổi có các tỉ lệ ban đầu như nhau thì các toạ độ D/S - N/S (tỉ lệ đồng vị đo được) sẽ nằm trên một đường thẳng có tuổi như nhau, được gọi là đường đẳng thời. Tuổi có thể tính được theo góc nghiêng của đường đẳng thời:

t = (1/l) ´ ln (độ nghiêng +1) (5.10)

Còn giao điểm với trục y (tức trục D/S) khi x = 0 (tức N/S = 0) là tỉ lệ đồng vị ban đầu (D₀/S)_i

Một thế mạnh của việc áp dụng phân tích đồng quy tuyến tính là có khả năng đánh giá thống kê độ chính xác của phép đo tuổi và tỉ lệ đồng vị ban đầu. Phương pháp hồi quy "bình phương nhỏ nhất" làm tối thiểu hoá sai lệch hoặc theo trục y hoặc theo trục x so với đường thẳng, các thông số của đường này là độ nghiêng và giao điểm với trục tung.

Phương trình để tính độ nghiêng (d) và giao điểm (b) của đường thẳng gần đúng có dạng:

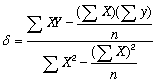và b =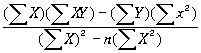

ở đây Y là tỉ lệ D/S (đồng vị con), X là tỉ lệ N/S (đồng vị mẹ) và n - số điểm trên đồ thị.

Phương pháp bình phương bé nhất dựa trên giả thiết cho rằng, sự sai lệch của các điểm ra khỏi đường thẳng chỉ do sai số theo trục y, còn theo trục x không có sai số. Rõ ràng giả thiết này không thật phù hợp để vẽ đường đẳng thời, bởi vì cả hai toạ độ, cả x lẫn y, đều chịu ảnh hưởng của sai số phân tích gây nên. Sự sai chệch của một số điểm ra khỏi đường gần đúng được thể hiện ở trị số "Bình phương trung bình của độ lệch trọng lượng" (Mean Squares of Weighted Deviates - MSWD). Trị số này được xem như thước đo độ chính xác của đường đẳng thời.

Trong trường hợp khi MSWD = 1, tất cả các tỉ lệ đo được phù hợp với đường gần đúng trong phạm vi sai số phân tích của phép đo. Nếu MSWD < 1, điều đó có nghĩa các phép đo được thực hiện với độ chính xác nhỏ hơn so với mong muốn. Nếu MSWD > 1, thì các tỉ lệ đo được chệch khỏi đường gần đúng lớn hơn so với mong đợi.

Đường thẳng có MSWD = 1 được gọi là đường đẳng thời thật. Nếu trị số MSWD lớn thì đường thẳng không phải là đường đẳng thời theo đúng nghĩa của từ này, vì các điểm bị phân tán không thể giải thích chỉ do sai số phân tích gây nên.

Bản chất sự phân tán các điểm trên đường đẳng thời rất quan trọng để luận giải các tài liệu địa thời. Nếu MSWD 2,5 thì sự phân tán có thể liên quan tới các sai số phân tích, nếu MSWD > 2,5, thì chắc có các nguyên nhân địa chất. Trong trường hợp sử dụng một loạt 4-6 khoáng vật, có thể xem giới hạn trên của sự hiệu chỉnh đường đẳng thời ứng với MSWD = 2,5 (theo Brooks và nnk., 1972). Đối với đường gần đúng có MSWD > 2,5, thường được gọi là đường lệch thời (errochrone).

Các đồng vị mẹ và con, các đồng vị để chuẩn hoá và các hằng số phân rã phóng xạ được sử dụng trong các phương pháp Rb-Sr, Sm-Nd và Re-Os xác định tuổi được thể hiện trong Bảng 5.1.

Bảng 5.1. Các thông số dùng trong các phương pháp Rb-Sr, Sm-Nd, Re-Os xác định tuổi

Phương pháp	Đồng vị sử dụng			Các hằng số phóng xạ			Biểu đồ đẳng thời
	Mẹ	Con	Bền vững (chuẩn hoá)	T1/2 (tỉ năm)	l (năm^-^1)	Kiểu phân rã	Trục X	Trục Y
Rb-Sr	^87Rb	^87Sr	^86Sr	48,8	1,42´10^-11	b^-	^87Rb/^86Sr	^87Sr/^86Sr
Sm-Nd	^147Sm	^143Nd	^144Nd	106	6,54´10^-12	a	^147Sm/^144Nd	^143Nd/^144Nd
Re-Os	^187Re	^187Os	^186Os	42,3	1,61´10^-11	b^-	^187Re/^186Os	^187Re/^186Os

Phương pháp Rb-Sr định tuổi

Rubidi là kim loại kiềm thuộc nhóm IA (gồm có Li, Na, Rb, Ce và Fr). Bán kính ion của nó (1,48 A^o) xấp xỉ bán kính ion kali (1,33 A^o), vì thế Rb thay thế K trong tất cả các khoáng vật chứa kali, như mica (muscovit, biotit, phlogopit, và lipidolit), felspat-K, một số khoáng vật sét và evaporit (silvin, carnalit).

Rubidi có hai đồng vị tự nhiên ⁸⁵Rb và ⁸⁷Rb với độ phổ biến tương ứng 72,1654% và 27,8346%. Khối lượng nguyên tử của nó là 85,46776 đơn vị khối lượng nguyên tử (a.e.m). ⁸⁷Rb phóng xạ và phân rã tạo ra đồng vị ⁸⁷Sr bền vững bằng cách phát xạ các hạt b^- theo phương trình ⁸⁷Rb đ⁸⁷Sr + b^-+ n + Q; ở đây b^- là hạt beta, n - antineutrino và Q- năng lượng phân rã.

Stronti thuộc nhóm nguyên tố kiềm-đất IIA (gồm có Be, Mg, Ca, Sr, Ba và Rd). Bán kính ion của Sr (1,13 A^o) hơi lớn hơn so với calci (0,99A^o) thường được thay thế trong nhiều khoáng vật như plagioclas, apatit, và carbonat calci, đặc biệt aragonit.

Stronti có 4 đồng vị bền vững (⁸⁸Sr, ⁸⁷Sr, ⁸⁶Sr, ⁸⁴Sr). Độ phổ biến tương ứng lần lượt vào khoảng 82,53; 7,04; 9,87 và 0,56%. Mức độ phổ biến của các đồng vị Sr thay đổi do có liên quan với sự thành tạo đồng vị phóng xạ ⁸⁷Sr khi phân rã đồng vị tự nhiên ⁸⁷Rb. Do đó thành phần đồng vị chính xác của Sr trong đá hoặc khoáng vật, có chứa Rb, phụ thuộc vào tuổi và tỉ lệ Rb/Sr trong đá hoặc khoáng vật này. Cần chú ý trong số bốn đồng vị stronti thì ⁸⁶Sr là ổn định về số lượng, nó là đồng vị bền, không xuất hiện do phân rã đồng vị tự nhiên của nguyên tố nào khác.

Trong quá trình kết tinh phân dị magma, Sr có khuynh hướng tập trung trong plagioclas, trong khi đó Rb còn tích lại trong pha lỏng. Do đó trong quá trình kết tinh tiến triển tỉ lệ Rb/Sr trong magma tàn dư có thể dần dần tăng lên.

Theo các thông số trong Bảng 5.1, phương trình (5.9) có thể được viết cụ thể đối với hệ Rb-Sr như sau:

⁸⁷Sr/⁸⁶Sr = (⁸⁷Sr/⁸⁶Sr)_i + ⁸⁷Rb/⁸⁶Sr (e ^lt - 1) (5.11) Suy ra: 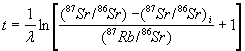(5.12)

Để tính được t (tức là tuổi của khoáng vật hoặc đá chứa Rb) theo biểu thức (5.12), cần đo được hàm lượng Rb và Sr và tỉ lệ ⁸⁷Sr/⁸⁶Sr. Hàm lượng Rb và Sr thường được đo hoặc bằng phương pháp huỳnh quang tia X, hoặc bằng phương pháp bổ sung đồng vị; tỉ lệ ⁸⁷Sr/⁸⁶Sr được đo trên khối phổ kế. Còn tỉ lệ ⁸⁷Rb/⁸⁶Sr được tính theo phương trình:

(5.13)

ở đây ⁸⁷Rb/⁸⁶Sr - tỉ lệ nguyên tử của các đồng vị này trong khoáng vật tại thời điểm hiện tại; (Rb/Sr) - tỉ lệ hàm lượng theo khối lượng của các nguyên tố này; P(⁸⁷Rb) và P(⁸⁶Sr) - độ phổ biến các đồng vị ⁸⁷Rb và ⁸⁶Sr; M(Rb) và M(Sr) - khối lượng nguyên tử tương ứng. Cần chú ý mức độ phổ biến ⁸⁶Sr và khối lượng nguyên tử của Sr phụ thuộc vào độ phổ biến của ⁸⁷Sr, vì thế các trị số tương ứng cần phải tính toán cho mỗi một mẫu. Khi tính toán cần sử dụng các trị số tỉ lệ đồng vị do Uỷ ban Địa thời học của Hiệp hội Địa chất quốc tế đề nghị năm 1976: ⁸⁶Sr/⁸⁸Sr = 0,1194; ⁸⁴Sr/⁸⁶Sr = 0,056584 và ⁸⁵Rb/⁸⁷Rb = 2,59265 và độ phổ biến các đồng vị dẫn ra ở trên.

Dưới đây minh hoạ cách tính toán qua ví dụ: Tính tỉ lệ nguyên tử ⁸⁷Rb/⁸⁶Sr cho mẫu biotit có hàm lượng Rb = 465 ppm, Sr = 30 ppm và tỉ lệ ⁸⁷Sr/⁸⁶Sr = 2.500.

- Trước hết tính độ phổ biến của các đồng vị và khối lượng nguyên tử Sr

Từ số liệu đã biết có thể tính được (nhờ phép nhân hoặc chia đẳng thức) (Bảng 5.2)

Bảng 5.2

Tỉ lệ đồng vị	Đồng vị	Độ phổ biến (3)	Khối lượng ng. tử (4)	(3) ´ (4)
87/88 = 0,2985	87	0,209524	86,9088 a.e.m	18,209 a.e.m
86/88 = 0,1194	86	0,083810	85,9092 a.e.m	7,200 a.e.m
84/88 = 0,006756	84	0,004742	83,9134 a.e.m	0,398 a.e.m
88/88 = 1,000000	88	0,701924	83,9134 a.e.m	61,703 a.e.m
Tổng = 1,424656		1,000000		87,510 a.e.m

Độ phổ biến ⁸⁶Sr trong mẫu này bằng 0,08381 hoặc 8,381% nguyên tử.

Khối lượng nguyên tử của nguyên tố được thể hiện ở đơn vị khối lượng nguyên tử (a.e.m), tương ứng 1/12 khối lượng của đồng vị ¹²C. Khối lượng nguyên tử của một nguyên tố là tổng khối lượng của các đồng vị tự nhiên của nó. Do đó trong bài toán ví dụ này khối lượng nguyên tử của Sr bằng 87,510 đơn vị khối lượng nguyên tử.

- Tính tỉ lệ ⁸⁷Rb/⁸⁶Sr theo công thức (5.13):

(⁸⁷Rb/⁸⁶Sr) =

Hậu quả kết tinh phân đoạn magma và tách các tinh thể khỏi dung thể tàn dư dẫn đến thành tạo một loạt các đá cùng magma có thành phần hoá học khác nhau. Nếu Sr trong magma này đồng nhất về đồng vị trong suốt thời kì nguội lạnh, thì tất cả các đá khác nhau, được thành tạo từ magma này, sẽ có tỉ lệ ⁸⁷Sr/⁸⁶Sr ban đầu như nhau. Hơn nữa thời gian để kết tinh magma tương đối không dài và các đá được xem cùng tuổi. Trong điều kiện như thế phương trình (5.11) là phương trình của một nhóm đường thẳng. Tất cả các mẫu của đá thuộc seri cùng magma, trên biểu đồ có toạ độ ⁸⁷Sr/⁸⁶Sr (y) và ⁸⁷Rb/⁸⁶Sr (x) nằm trên đường thẳng "đẳng thời", bởi vì tất cả các điểm trên đường này phù hợp với các hệ có cùng một tuổi t và cùng một tỉ lệ ⁸⁷Sr/⁸⁶Sr ban đầu.

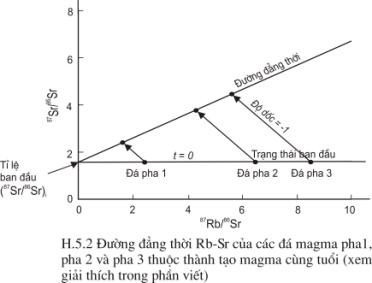
Cơ sở của phương pháp xây dựng đường đẳng thời có thể thấy rõ trong ví dụ sau đây: tiến hoá đồng vị của Sr của seri gồm 3 mẫu đá magma giả định được thành tạo từ magma chung và có các tỉ lệ Rb/Sr khác nhau được thể hiện trên Hình 5.2. Trong thời gian kết tinh các điểm của 3 mẫu đá nằm trên đường thẳng, tang của góc nghiêng của đường thẳng này bằng không, bởi vì tất cả chúng có cùng một tỉ lệ ⁸⁷Sr/⁸⁶Sr. Sau khi nguội lạnh đến nhiệt độ mà ở đó các đá này thành tạo hệ kín, tỉ lệ ⁸⁷Sr/⁸⁶Sr trong chúng bắt đầu tăng do phân rã ⁸⁷Rb để thành tạo ⁸⁷Sr. Mỗi hành vi phân rã ⁸⁷Rb làm giảm tỉ lệ ⁸⁷Rb/⁸⁶Sr, đồng thời làm tăng tỉ lệ ⁸⁷Sr/⁸⁶Sr với cùng một mức.

Do đó những tỉ lệ này được dịch chuyển dọc theo đường thẳng có tang góc nghiêng bằng -1 (âm 1), như vậy các điểm của mẫu đá sẽ còn lại trên đường đẳng thời, trong khi đó độ nghiêng của nó sẽ tăng lên theo hàm số của thời gian. Tuy nhiên điểm giao cắt của đường đẳng thời với trục y khi đó không thay đổi và tương ứng với tỉ lệ ⁸⁷Sr/⁸⁶Sr ban đầu của seri các đá.

Để định tuổi của các đá cùng magma bằng phương pháp đẳng thời theo các đá nói chung, cần phải lấy một seri mẫu đá, seri này bao quát khoảng rộng tỉ lệ Rb/Sr để xác định chắc chắn độ nghiêng của đường đẳng thời. Sau khi nhận được các kết quả phân tích cần thiết (chúng tôi khuyến cáo nên tính toán kiểm tra ⁸⁷Rb/⁸⁶Sr theo công thức 5.13), các tài liệu được đưa lên đồ thị có toạ độ ⁸⁷Sr/⁸⁶Sr - ⁸⁷Rb/⁸⁶Sr. Sau đó vẽ đường hồi quy tuyến tính (đường đẳng thời) đi qua các điểm thể hiện các mẫu phân tích, xác định độ nghiêng của đường đẳng thời và giao điểm của nó với trục tung. Ngày nay, những công việc vừa nêu được xử lí dễ dàng bằng phần mềm Igpetwin, Minpet hoặc bằng phần mềm Isoplot chuyên xử lí các tài liệu đồng vị. Tuổi của seri đá được tính theo độ nghiêng bằng công thức (5.10). Trị số t tính được trong phần lớn trường hợp xác định thời gian kết tinh ban đầu từ magma của các đá.

Phương pháp Sm-Nd định tuổi

Neodim (Z = 60) và Samari (Z = 62) là các nguyên tố đất hiếm nhẹ thuộc nhóm IIIB của hệ thống tuần hoàn cùng với itri và scandi. Bán kính ion của chúng bằng 1,08 A^o (Nd ⁺³) và 1,04 A^o (Sm ⁺³).

Samari có 7 đồng vị tự nhiên, còn neodim có 7 đồng vị bền. Cả hai nguyên tố này chứa các đồng vị mẹ và con:

+ a + Q với T_1/2 = 1,06´10¹⁰ năm

+ a + Q với T_1/2 = 1,8´10⁶ năm

+ a + Q với T_1/2 = 1,0´10⁸ năm

ở đây Q - năng lượng phân rã và T_1/2 - chu kì bán phân rã.

Theo phương trình (5.9) và các thông số trong Bảng 5.1, phân rã ¹⁴⁷Sm thành ¹⁴³Nd được viết cụ thể trong hệ Sm-Nd:

(¹⁴³Nd/¹⁴⁴Nd) = (¹⁴³Nd/¹⁴⁴Nd)_i + (¹⁴⁶Sm/¹⁴⁴Nd)(e^lt -1) (5.14)

ở đây với l = 6,54´10^-12 và ¹⁴⁴Nd được sử dụng như là đồng vị so sánh, bởi vì số lượng nguyên tử ¹⁴⁴Nd trong một đơn vị khối lượng đá hoặc khoáng vật không thay đổi, trong khi đó hệ là kín đối với Nd.

Xác định tuổi bằng phương pháp Sm-Nd thường tiến hành phân tích các khoáng vật tách hoặc phân tích một seri đá, có tỉ lệ Sm/Nd biến thiên đủ lớn tạo ra độ nghiêng của đường đẳng thời trong hệ toạ độ ¹⁴³Nd/¹⁴⁴Nd (y) và ¹⁴⁶Sm/¹⁴⁴Nd (x). Các đường đẳng thời Sm-Nd dựa trên cùng luận cứ đã được trình bày kĩ ở phương pháp Rb-Sr. Cần chú ý các đường đẳng thời khoáng vật Sm-Nd và Rb-Sr cho phép phán đoán tuổi kết tinh của các đá magma. Điều này chỉ có thể khi tổ hợp cộng sinh các khoáng vật là đảm bảo chắc chắn, hay nói cách khác, các khoáng vật được thành tạo cân bằng với nhau trong một giai đoạn, mà không phải do kết quả của một vài giai đoạn tách rời nhau về mặt thời gian. Để kiểm soát có sự phá huỷ quan hệ đồng vị trong các khoáng vật hay không, cần phân tích một mẫu đá tổng. Và nếu mẫu này là một trong các điểm trên đường đẳng thời của các khoáng vật, thì chứng tỏ các khoáng vật cân bằng trong một hệ. Khi biến đổi nhiệt dịch hoặc phong hoá trên mặt có thể phá huỷ hệ thống đồng vị trong khoáng vật, khiến các xác định tuổi không chính xác. Vì thế tiêu chuẩn tươi là tiêu chuẩn hàng đầu khi lựa chọn các khoáng vật để xác định tuổi. Ngoài ra hệ thống đồng vị bị phá vỡ do các đồng vị phóng xạ bị khuyếch tán mà không gây ra sự biến đổi nào thấy được ở các khoáng vật.

Phương pháp Sm-Nd tốt nhất được dùng để định tuổi của các đá bazơ và siêu bazơ, trong khi đó phương pháp Rb-Sr dùng cho các đá thành phần axit và trung tính. Ngoài ra các nguyên tố đất hiếm kém linh động hơn các nguyên tố kiềm và kiềm thổ trong biến chất khu vực, biến đổi nhiệt và phong hoá hoá học. Vì thế các đá có thể định tuổi chắc chắn bằng phương pháp Sm-Nd, thậm chí nếu chúng thu nhận hoặc mất Rb và Sr. Như vậy phương pháp Sm-Nd có thể dùng để xác định tuổi các đá, không thuận lợi để định tuổi bằng phương pháp Rb-Sr hoặc do tỉ lệ Rb/Sr thấp, hoặc do chúng không còn là hệ kín đối với Rb và Sr.

Phương pháp Re-Os định tuổi

Reni có số nguyên tử là 75, cùng với Mn và Tc trong phụ nhóm VIIB của hệ thống tuần hoàn Mendeleev. Reni là nguyên tố phân tán gặp hầu hết trong các khoáng vật của các nguyên tố khác, tập trung cao nhất trong molybdenit - từ một vài phần triệu đến 1,88%. Trong các molybdenit đi cùng với các khoáng vật sulphur đồng, hàm lượng Re thường rất cao.

Osmi có số nguyên tử 76 - là kim loại nhóm platin thuộc phụ nhóm VIIIB của hệ thống tuần hoàn. Reni là nguyên tố siderophil và gặp chủ yếu trong khoáng vật Osmirid.

Reni có hai đồng vị tự nhiên ¹⁸⁵Re và ¹⁸⁷Re với độ phổ biến của chúng là 37,398 và 62,602. Khối lượng nguyên tử của Re là 186,20679 ± 0,00031 a.e.m. ¹⁸⁷Re phóng xạ và chuyển thành ¹⁸⁷Os bền bằng phát xạ hạt b^-:

Osmi có 7 đồng vị tự nhiên, tất cả chúng đều bền vững. Độ phổ biến của các đồng vị Os là: ¹⁸⁴Os = 0,0239%; ¹⁸⁶Os = 1,600%; ¹⁸⁷Os = 1,510%; ¹⁸⁸Os = 13,286%; ¹⁸⁹Os = 16,251%; ¹⁹⁰Os = 26,369% và ¹⁹²Os = 40,957%. Khối lượng nguyên tử của Os bằng 190,2386.

Theo phương trình tổng quát (5.9), đối với hệ Re-Os có dạng:

(¹⁸⁷Os/¹⁸⁶Os) = (¹⁸⁷Os/¹⁸⁶Os)_i + (¹⁸⁷Re/¹⁸⁶Os)(e^lt-1) (5.15)

Các tài liệu phân tích của một seri mẫu có cùng tuổi và cùng tỉ lệ ¹⁸⁷Os/¹⁸⁶Os ban đầu được đưa lên hệ toạ độ ¹⁸⁷Os/¹⁸⁶Os - ¹⁸⁷Re/¹⁸⁶Os để xây dựng đường đẳng thời, tang góc nghiêng của nó tỉ lệ với tuổi của các mẫu. Giao điểm của đường đẳng thời với trục tung xác định tỉ lệ ban đầu (¹⁸⁷Os/¹⁸⁶Os)_i.

Phương pháp Re-Os dùng để xác định tuổi trực tiếp các mỏ khoáng. Trong molybdenit Re có lượng lớn, trong khi đó không chứa Os ban đầu, vì thế phương trình (5.15) để định tuổi molybdenit theo phương pháp Re-Os có thể viết lại đơn giản hơn:

(¹⁸⁷Os/¹⁸⁶Os) = (¹⁸⁷Re/¹⁸⁶Os)(e^lt - 1), từ đây suy ra:

(¹⁸⁷Os/¹⁸⁷Re) = (e^lt - 1) với l = 1,61´10^-11năm^-1 (5.16)

Bởi vì trong các mẫu tự nhiên ¹⁸⁷Re luôn chiếm 1,60% của tổng tất cả các đồng vị Re, nên khi định tuổi của molybdenit không cần phải xác định thành phần đồng vị của Re. Còn hàm lượng tuyệt đối của ¹⁸⁷Os được xác định bằng phương pháp khối-phổ kế bổ sung đồng vị. Vì thế việc định tuổi molybdenit được đơn giản đi rất nhiều.