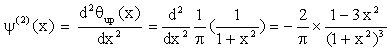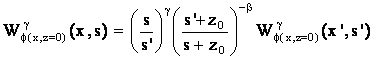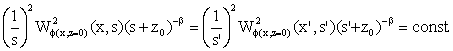USING THE POISSON-HARDY WAVELET TO DETERMINE THE SOURCE
PROPERTIES FOR THE MAGNETIC ANOMALIES OF MEKONG
DELTA
1DƯƠNG HIẾU ĐẬU, 1TRƯƠNG
THỊ BẠCH YẾN, 2ĐẶNG VĂN LIỆT
1Cần Thơ University,
Cần Thơ City,
2University of Sciences, Việt
Nam National
University, Hồ Chí Minh City
Abstract: Determination of source properties for
the gravity and magnetic data is an important role in the inverse potential
field problems. In recent years, several researchers have been successfully
using the method based on the continuous wavelet transform with wavelet
functions made of the first horizontal derivatives of Poisson kernel to
estimate the horizontal location and the depth of the sources. In this paper,
the authors construct the Poisson-Hardy wavelet to determine the position of
sources and then use the relations of multi-scale continuous wavelet transform
to calculate the structural index of simple homogeneous anomaly sources. The
results of this estimation on the magnetic data of the Mekong
Delta are compatible with the results of the other methods.
I. INTRODUCTION
In the 1980’s decade, Thompson et al. [13] provided the solution for the inverse
problem of magnetic prospecting using the method called as “Euler convolution”.
They also introduced a concept about the structural index N or “attenuation
rate” of the simple, homogeneous magnetic sources. In the next decade, Moreau et al. [6, 7],
Sailhac et al. [9, 10, 11], and Fedi et al. [4] described an interpretation
technique based on continuous
wavelet transform (CWT) and the Poisson wavelet families to estimate the homogeneous structure of the simple
magnetic anomalies. In this item, we have proposed a suitable wavelet function named as Poisson-Hardy wavelet [1] to determine the position and the depth
of the magnetic sources. In this paper,
the authors also apply the real part of this wavelet function to the Moureau’s theory [6] to determine the
structural index N of magnetic sources.
II. CONTINUOUS POISSON-HARDY WAVELET FUNCTION
The continuous wavelet transform of 1-D signal f(x)Î L2(R) can be given by:
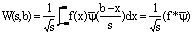 (1)
(1)
Where, s, b Î R+ are
scale and translation (shift) parameters; L2(R) is the Hilbert space
of 1-D wave functions having finite energy; 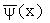 is the complex conjugate function of y(x), an analyzing function inside the integral (1). In particularly,
CWT can operate with various complex wavelet functions, if the wavelet function looks like the same form
of the original signal.
is the complex conjugate function of y(x), an analyzing function inside the integral (1). In particularly,
CWT can operate with various complex wavelet functions, if the wavelet function looks like the same form
of the original signal.
Using the method based on
Multi-Edge Detection (MED) to determine the horizontal positions and depth of
magnetic sources, we designed a complex
wavelet function from the Poisson kernel of the upward continuation filtering (Blakely) [2]. The upward continuation filtering is given by the
well-known Dirichlet integral:
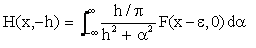 (2)
(2)
Where, H(x, -h) is the
field measured on a plane a distance h above the datum plane (z = 0); F(x,0) is
the field measured on the datum plane, and:
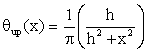 (3)
(3)
is
the Poisson
kernel, that plays the role
of smoothing function.
For the MED method, the position
and the depth of the gravity/magnetic source were determined
by local
maxima points corresponding to the
wavelet function transform y(1) (the first derivative of
the smoothing function) or inflection points (called ‘zero crossing’ points)
corresponding to the wavelet function transform y(2) (the second derivative of the smoothing function).
The y(1) and y(2) are given:
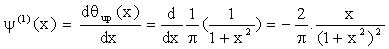 (4)
(4)
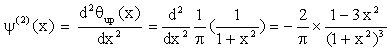 (5)
(5)
Grosman et al. [3] proposed
a process to compute the “zero
crossing” points using the phase of a complex wavelet function called as “Hardy wavelet” form:
y(4) =
y(2) +
i y(3)
(6)
Where, y(3)(x)
is the Hilbert transform of y(2)(x). In this paper y(3) is given as:
 (7)
(7)
Here, we put h = 1 in the formula
(4), (5) and (6) to satisfy the wavelet function conditions. From equations (5)
and (7), we construct a new complex wavelet function named as Poisson-Hardy
wavelet function as type (6) [1].
III. DETERMINATION OF STRUCTURAL INDEX
According to the Thompson’s theory [13], the homogeneous field source f(x, y, z) can be expressed as following equation for any constant l non zero:
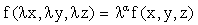 (8)
(8)
Where, a is a coefficient of homogeneity, that is related to the structural index of the magnetic source by the relation:
 (9)
(9)
The Table 1 shows the structural index of various simple magnetic sources
written by Reid [8].
According to Moreau et al. [6], we denote f(x, z = 0) as measuring
data in the ground (z = 0) due to a homogeneous source
located at x = 0, z = z0 with the structural index N. When we carry out the
continuous wavelet transformation on measuring data with the wavelet functions
that are the horizontal derivative of qup(x) we obtain an equation related to the wavelet
coefficients at two scale levels s and s’:
Table 1. Structural
index for various homogeneous magnetic sources
|
No
|
Type of sources
|
N
|
|
1
|
Sphere
|
3
|
|
2
|
Vertical cylinder
|
2
|
|
3
|
Horizontal cylinder
|
2
|
|
4
|
Dike
|
1
|
|
5
|
Contact or Fault
|
0
|
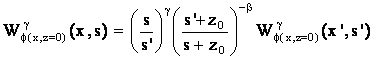 (10)
(10)
Where, b = (a - g) (11)
With g being the order of derivatives of analyzing wavelet functions, N can be calculated
from (9) and (11):
N = - b - g - 1 (12)
For
different positions x and x’, the relation of scale parameters s and s’ is given [6] as follows:
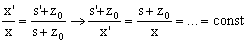 (13)
(13)
In this paper, we determine the structural index N of anomaly
sources by the continuous wavelet transform
with the wavelet function y2 (g =
2), Thus we can rewrite the equation (10) as follows:
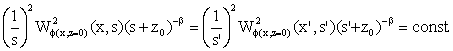 (14)
(14)
Using short notation 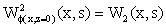 and taking the
logarithm for both sides of (14), we
derive a new expression:
and taking the
logarithm for both sides of (14), we
derive a new expression:
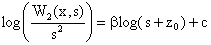 (15)
(15)
Where, c is the constant related to the const. in the right side
of equation (14). The structural index determination will be done by
the estimation for the slope of a straight line:
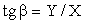 (16)
(16)
Where, 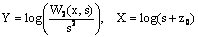
IV. EXPERIMENTAL MODEL
The magnetic source is a cylinder
hollow iron tank with the length and radius of 120 cm and 80 cm, respectively.
It was buried in a shallow ditch so that the level of the tank top is the
ground surface (Fig. 1). The measurement profile is perpendicular to the strike
of the tank and the length of the profile is about 30 m long, with the step size of 0.5 m. The PM-2 proton
magnetometer with the accuracy up to 1.0 nT was used. The sensor was hold at
the altitude of 2 m from the ground, so the position of the source is: x = 0, z
= 2 m.
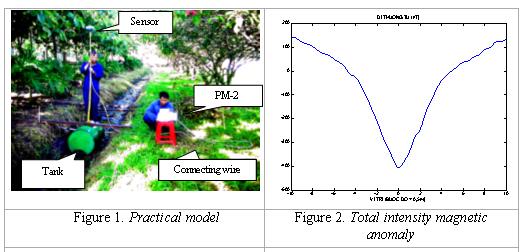
The total intensity
magnetic anomaly of the tank is showed in Fig. 2. The determination of the
horizontal position and the depth of the souce comprise two steps: a) computing
the first horizontal gradients, and b) computing the wavelet transform of the first
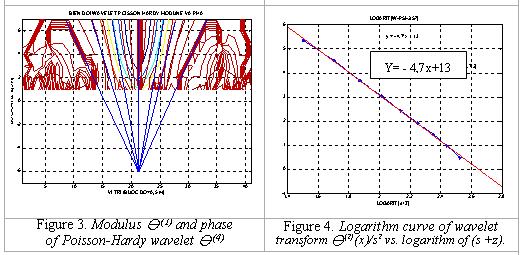
horizontal gradient with y(1) and y(4), respectively. Fig. 3
shows the modulus of y(1) and phase of Poisson-Hardy
wavelet y(4), this figure is an useful tool
to determine the position and the depth of the tank. The result (x = 0, z = 2m)
shows that, it is suitable with the position and the depth of the model.
Fig. 4 shows the logarithm curve of wavelet transform y(2)(x)/s2 vs. to
logarithm of (s+z). In the Fig. 4, using least square method, we get the
equation for a straight line: Y = - 4,7x
+ 13, then we estimate b » -5, so the structural index is N
= 2 (Equ. 12, g = 2). It is suitable with the tank model having the
cylinder shape (N = 1, Table 1).
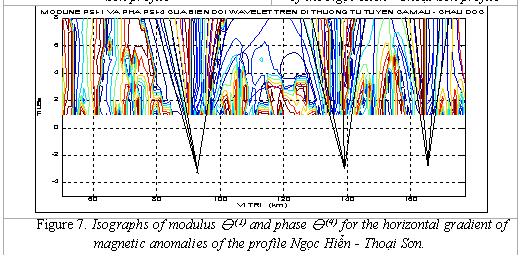
V. INTERPRETATION OF MAGNETIC DATA FROM THE MEKONG DELTA
The total intensity of
aeromagnetic map at the 1/500.000 scale (Department of Geology and Minerals of Việt
Nam)
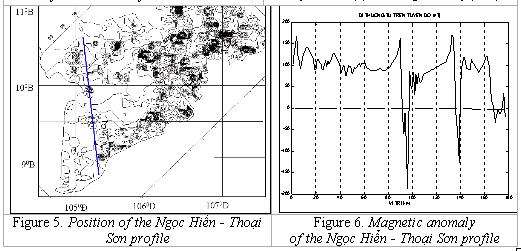
has been used. In this map we slice a profile 177 km long from Ngọc Hiển (Cà Mau)
to Thoại Sơn (Châu Đốc), then the data are interpolated into regular points
(step size 1.0 km) by cubic spline. Using the International Geomagnetic
Reference Field (IGRF) from Kyoto
University, we calculate
the total intensity magnetic anomalies of the profile; the results are showed
in Fig. 6.
The Fig. 7
shows the modulus y(1) and phase y(4) of the horizontal gradient of magnetic anomalies of the
profile Ngọc Hiển - Thoại Sơn. There
are 3 anomaly sources of this profile and the results are presented in Table 2.
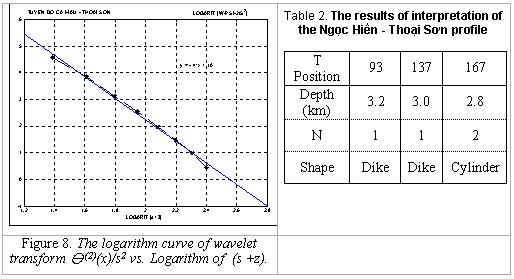
Fig.
8 is the logarithm curve of wavelet transform [y(2)(x)]/s2 vs. to
logarithm of (s+z) of the anomaly source
located at position of 137 km. Using the least square method to determine the
equation of linear line Y = - 4.0 + 10,
so b » - 4 (Equ. 16) so
the
structural index is N = 1 (Equ. (12), g -2). Consequently, the source may be a dyke (Tab. 2).
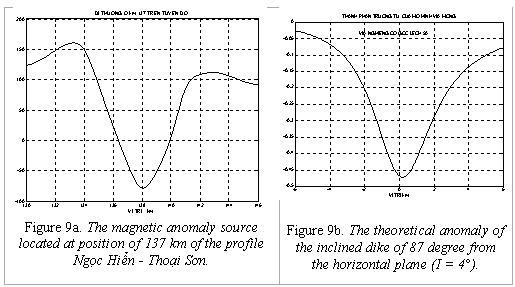
For verifying the result, we present the magnetic anomaly of the anomaly located at
position of 137 km from x = 130 km to x = 146 km in Fig. 9a. We also computed the theoretical model
of the magnetic anomaly of an inclined dyke 87o from the horizontal plane with the inclination I = 4o (the values is the average
value of inclination of Mekong delta area) (Fig. 9b). The two
Fig. 9a and 9b are similar, so they prove the reasonable result for the estimated structural index (Fig. 8). In addition, the angle of the
theoretical inclined dike could be recognized as the inclined source located at position of 137 km.
VI. CONCLUSIONS
We used the
Poisson-Hardy wavelet function came from the second derivative of the kernel of
the upward continuation filtering to solve the inverse problem of potential
field with the determination of the positions, depths and structural index. The
results of the experimental model show that the interpretation using
Poisson-Hardy gives a good result. We interpreted also the Ngọc Hiển - Thoại Sơn
magnetic anomaly profile, the results show that there are two anomaly sources with the dike form and one
source having the cylindric form.
Since this method can only be applied
for the simple and separate sources, we could not determine the depths and the
structural index of some anomaly sources near by. This technique will be
improved for further research to interpret closed sources.
REFERENCES
1. Dương
Hiếu Đậu, Trần Ngọc Chánh, Đặng Văn Liệt, 2007. Dùng phương pháp tính biên đa tỉ lệ MED (multiscale edge detection) để xác
định vị trí và độ sâu của các dị thường từ ở vùng Nam Bộ. TC Khoa học, Đại học Cần Thơ, số 08-2007.
2. Blakely R.J., 1996. Potential theory in gravity and magnetic applications. Cambridge Univ.
Press, New York.
3. Grossman A., Hoschneider M.,
Kronland, Martinet R., Morlet J., 1987. Detection of abrupt changes in sound signals with the
help of wavelet transforms. Inverse
Probl., 19: 281-306. Acad. Press, New
York.
4. Fedi
M., Primiceri R., Quata T., Villani A.V., 2004. Joint application of continuous and discrete
wavelet transform on gravity data to identify shallow and deep sources. J. of Geoph.
Inc., 156: 7-21.
5. Moreau F.,
1995. Méthodes de
traitement de données géophysiques par transforme en ondelettes. Thèse de Dr., Univ. de Rennes I. Rennes,
France. pp.177.
6.
Moreau F., Gibert D., Holschneider M., Saracco G., 1997. Wavelet analysis of potential
fields. Inverse Probl., 13: 165-178.
Acad. Press, New York.
7.
Moreau F., Gibert D., Holschneider M., Saracco G., 1999. Identification of sources of
potential fields with the continuous wavelet transform: Basic theory, J. of Geoph. Res., 104/B3: 5003-5013.
8. Reid A.B., Allsop
J.M., Granser H., Millet A.J., Somerton I.W., 1990.
Magnetic interpretation in
three dimensions using Euler deconvolution. Geophysics, 55: 80-91.
9. Sailhac P.,
1999. Analyse
multiéchelle et inversion de données géophysiques en Guyane Française. Ph.D.
Thesis, Inst. de Phys. du Globe de Paris.
10.
Sailhac P., Gaeano, A., Gibert D., Moreau F., Delor C., 2000. Identifica-tion of sources of potential fields with the continuous
wavelet transform: Complex wavelets and applications to magnetic profiles in
French Guyana. J. of Geophys.
Res., 105: 19455-19475.
11. Sailhac P., Gibert D., 2003. Identification of sources of potential fields with the continuous
wavelet transform: 2D wavelets and multipolar approximations. J. Geophys. Res., 108: 2296-2306.
12. Smith T.A., Dentith M.C., 1999. The wavelet transform in aeromagnetic processing. Geophysics, 64: 1003-1013.
13. Thompson D.T., 1982. EULDPH:
A new technique for making computer-assisted depth estimates from magnetic data. Geophysics, 47: 31-37.
![]() (1)
(1)![]() is the complex conjugate function of y(x), an analyzing function inside the integral (1). In particularly,
CWT can operate with various complex wavelet functions, if the wavelet function looks like the same form
of the original signal.
is the complex conjugate function of y(x), an analyzing function inside the integral (1). In particularly,
CWT can operate with various complex wavelet functions, if the wavelet function looks like the same form
of the original signal. ![]() (2)
(2)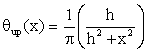 (3)
(3)