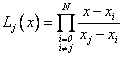Using
Mathematica the function 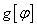 is defined as follows:
is defined as follows:
g
[phi]:=978.0318(1+0.0053024sin [phi degree]^2-0.00000sin[2phi degree]^2).
From
this formula, we may easily calculate the normal gravity values for different
latitudes without regarding standard table:
Table
[{phi,g[phi]},{phi,1,25,.5}]//InputForm
{{1, 978.0333795598982},
{2, 978.0381163151427}, {3, 978.0460044947265},
{4, 978.0570344881181},
{5, 978.0711928569697}, {6, 978.0884623514894},
{7, 978.1088219314587},
{8, 978.1322467918656}, {9, 978.1587083931254},
{10, 978.1881744958536},
{11, 978.2206092001427}, {12, 978.255972989302},
{13, 978.2942227780015},
{14, 978.3353119647657}, {15, 978.3791904887497},
{16, 978.4258048907312},
{17, 978.4750983782416}, {18, 978.5270108947595},
{19, 978.5814791928802},
{20, 978.6384369113727}, {21, 978.6978146560302},
{22, 978.7595400842176},
{23, 978.8235379930088}, {24, 978.8897304108098},
{25, 978.9580366923559}}.
Calling
ki being correction values for weight unit of each polygon,
according to [7], we have following equations for calculation of ki:
eq1 = 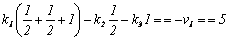
eq2 = 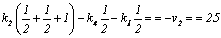
eq3 = 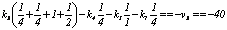
eq4 = 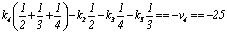
eq5 = 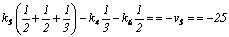
eq6 = 
eq7 = 
(2)
Solving
these equations with the aid of Mathematica (Solve[{eq1,eq2,eq3,eq4,eq5,eq6,eq7},{k1,k2,k3,k4,k5,k6,k7}])
we receive the ki values: k1=-21.5858, k2=-6.06507, k3=-45.1391, k4=-52.6745, k5=-53.2402, k6=-56.8574, k7=-62.0948.
Now, we calculate the
corrected gravity differences for all sides of network. We consider two cases:
single side and common side between two polygons. For example, we calculate:
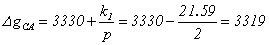
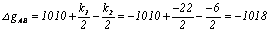
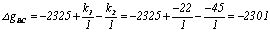
By similar method, we
calculate all corrected gravity differences for all sides of the network.
3. Interpolation, approximation and their
applications
Suppose 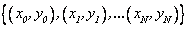 is a set of
geophysical data where x0<
x1<… <xN. We do not have an analytic expression
of a function f whose graph contains
these points, yet we want to calculate its value at an arbitrary point. For
this purpose, we find the polynomial PN(x)
of degree not higher than N, whose values
at point xi coincide with
the values of data, i.e. Pn(xi)=yi
[6]. In this paper, we use Lagrange’s
and Spline interpolations. Lagrange’s polynomial interpolation has the
following form [6]:
is a set of
geophysical data where x0<
x1<… <xN. We do not have an analytic expression
of a function f whose graph contains
these points, yet we want to calculate its value at an arbitrary point. For
this purpose, we find the polynomial PN(x)
of degree not higher than N, whose values
at point xi coincide with
the values of data, i.e. Pn(xi)=yi
[6]. In this paper, we use Lagrange’s
and Spline interpolations. Lagrange’s polynomial interpolation has the
following form [6]:
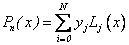 (3)
(3)
where 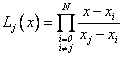 (4)
(4)
Spline interpolation uses
polynomial n degrees in intervals (xj, xj+1) and using
different conditions for calculating different coefficients in the polynomial.
In Mathematica, there are
2 commands for using interpolation: Interpolating-Polynomial [data, {vars}]; Interpolation [data].
The following table for
the simulation of gravity anomalies is given:
|
x
|
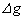 (mGal) (mGal)
|
x
|
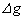 (mGal) (mGal)
|
|
-1000
-900
-800
-700
-600
-500
-400
-300
-200
-100
|
0.0284305
0.0329207
0.0385575
0.0457655
0.0551856
0.0678237
0.0853379
0.110644
0.149361
0.213976
0.338755
|
100
200
300
400
500
600
700
800
900
1000
|
0.612007
0.779651
0.826098
0.884819
0.748206
0.527098
0.354403
0.243304
0.17357
0.128626
|
With these data, Spline
interpolation is applied for receiving function 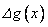 and
and  is calculated. Received results indicate the ability of using
interpolation approach in processing geophysical data.
is calculated. Received results indicate the ability of using
interpolation approach in processing geophysical data.
III. MATHEMATICA CAS IN THE COMPUTATION OF
GRAVITY ANOMALIES
Mathematica CAS may be
used in two ways in the computation of gravity anomalies. The first way
involves its use for contouring charts or templates which can then be manually
used for computation of anomalies. The second is for direct application in the
computation of the gravity and magnetic effect of bodies of arbitrary shape by
developing the expressions for attraction as recursive formulas that are
conveniently handled by computer.
1. Horizontal cylinder, horizontal line
element
We choose the coordinate
system of Fig. 3 such that the horizontal cylinder is parallel to the y axis
and has the parameters h and R.
In this system we have
[7]:
 (5)
(5)
For calculating the
gravity effect of horizontal cylinder, in Mathematica we may use the following
commands:
Clear
["Global`*"]; sl = {k->66.73 10^-7, sig->500; h->200,
R->100, x0->150};
f[x_] = 2k Pi R^2 sig
h/((x-x0)^2+h^2); Plot [f[x]/.sl, {x, -700, 700}].
2. Horizontal rectangular parallelepiped
Gravity effect of
rectangular parallelepiped is determined by following formula:
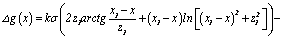
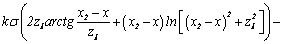
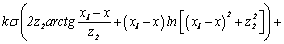
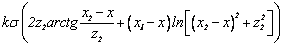 (6)
(6)
Results
of calculation by Mathematica for 2 horizontal rectangular parallelepipeds are
presented in Fig. 4:
Clear["Global`*"];
SetOptions[Plot, PlotStyle->Thick];
sl1 = {k->66.73 10^-7,
sig->100., x1->250., x2->400., z1->50., z2->350.};
sl2 = {k->66.73 10^-7,
sig->500., x1->750., x2->1500., z1->450., z2->750};
f[xi_, x_, z_] = k
sig((x-xi)log[(x-xi)^2+z^2]+2z ArcTan[(x-xi)/z]);
f1[xi_, x_] = f[xi, x,
z2]-f[xi, x, z1];
f2[xi_]=f1[xi, x2]-f1[xi,
x1];
p1 = Plot
[(f2[xi]/.sl1)+(f2[xi]/.sl2),{xi, -500, 2000}].
With
the similar way we may calculate the gravity effect of different shapes of
geological bodies.
IV. TRANSFORMATION OF GEOPHYSICAL DATA
The
main purpose of separation (transformation) of potential (gravity and magnetic)
fields is the extraction from observed field into components that are
associated with individual geological objects located at different depths. The
resulting function, depending on transformed operations may be of the same unit
of initial function or their derivatives. Derivatives of initial function may
be taken at started level or at new ones. The transformed function may have
unit of product of initial function and coordinates.
Before
eighty years, due to low technique and poor computing tool, most problems of
field transformation were mainly carried out in space domain. At present, these
problems, in general tendency, will be implemented in frequency domain with
assistance of Fast Fourier or of other software.
Transformation in Space
Domain
The
mathematical expression of popular field transformation in space domain can be
drawn out [5]:
-
Averaging: The average of observed field is taken within the circle of
radius R at the centre of circle:
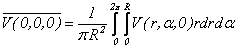 (7)
(7)
-
Analytical continuation of the field from 0-level to Z-level is
expressed by:
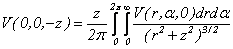 (8)
(8)
-
Derivatives undertaken along x-axis can be written:
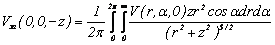 (9)
(9)
-
Derivatives calculated with respect to z-axis:
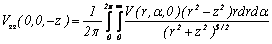 (10)
(10)
In
particular way, for calculating above-mentioned transformations, the palettes
designed for that purpose are used. Furthermore, these analytical expressions
are suitable for computer calculations.
Transformation is
carried out in frequency domain
In
this domain all above-mentioned transformations can be expressed in common
formulae:
- For 3D problems:
 (11)
(11)
-
For 2D cases:
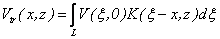 (12)
(12)
where:
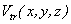 ,
,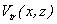 ,
, ,
,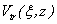 are initial fields;
are initial fields; 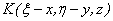 ,
, 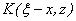 - transformation
kernels corresponding respectively to 3D or 2D problems.
- transformation
kernels corresponding respectively to 3D or 2D problems.
Expressions
(11) and (12), which are integrals of 2 functions, are called as convolution.
Mathematically, the process of signal filtering is described by such integrals.
That is the problems of potential field transformation that can be considered
as frequency filtering, in which various transformation operations are realized
with different frequency characteristics.
According
to the theory of convolution in the frequency domain, spectrum 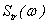 of function
of function 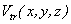 or
or 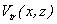 is the multiplication of ones of
is the multiplication of ones of 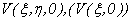 and
and 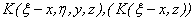 , i.e.
, i.e.
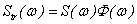 (13)
(13)
 (14)
(14)
where
 the spectrum of
functions is
the spectrum of
functions is 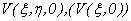 ,
, 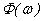 is spectrum (frequency
characteristics) of function
is spectrum (frequency
characteristics) of function 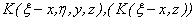 .
.
Using
direct Fourier transform, 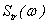 in formula (13) is
calculated and after that, by inverse Fourier transforms, function
in formula (13) is
calculated and after that, by inverse Fourier transforms, function 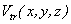 is determined. Table 1
gives the frequency characteristics for different transformations of potential
data.
is determined. Table 1
gives the frequency characteristics for different transformations of potential
data.
Table 1. Transformation
and its frequency characteristics
|
Transformation
|
Frequency
characteristics
|
|
- Average:
· 3D
Problem
· 2D
Problem
|
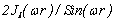 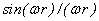
|
|
- Analytical Continuation
· Upward
continuation
· Downward
continuation
|
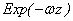

|
|
- Vertical derivatives of n-order
· On the
observed surface
· At the
height z
|
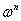
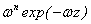
|
|
- Horizontal derivatives of n- order
· On the
observed surface
· At the
height z
|
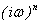
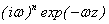
|
Transformation
methods in frequency domain are realized on received geophysical data with
accepted results.
V. CONCLUSIONS
We
have used Mathematica CAS for processing, calculation and enhancement of
geophysical data for determining their cause. Simulation results give us the
opportunities of their use in practice.
REFERENCES
1. Bahder T.B., 1995. Mathematica for scientists and engineers. Addison-Wesley Publ. Co.
2. Nikitin A.A., 1993.
Statistical processing of geophysical data.
Electromagnetic Res. Center, Moscow.
3. Sharma P.V., 1997. Environmental
and enginneering geophysics. Cambridge
Univ. Press.
4. Tafeev G.P, Sokolov K.P., 1981.
Geological interpretation of magnetic anomalies. Nedra, Leningrad.
5. Tôn Tích Ái, 1988.
Applied geophysics. Univ. Min. Publ., Hà
Nội.
6. Tôn Tích Ái, 2000.
Computational method. Nat. Univ. Publ.,
Hà Nội.
7. Tôn
Tích Ái, 2003. Gravity and gravity prospecting. Nat. Univ. Publ., Hà Nội.
8. Tôn Tích Ái, 2005.
Geomagnetism and magnetic prospecting.
Nat. Univ. Publ., Hà Nội.
9. Wolfram S., 1988.
Mathematica. Addison-Wesley Publ. Co.
![]() (GRS-1967). The formula is [3]
(GRS-1967). The formula is [3]