COMPUTATION OF WAVE FIELD IN THE ĐỒNG TRANH ESTUARY, CẦN GIỜ  BY USING WAVE REFRACTION MODEL

VÕ LƯƠNG HỒNG PHƯỚC, NGUYỄN ĐỨC TOÀN,
ĐẶNG TRƯỜNG AN, TRƯƠNG CÔNG HẠNH

University of Natural Sciences, Vietnam National University, Hồ Chí Minh City,
227 Nguyễn Văn Cừ, Dist. 5, HCMC. vlhphuoc@phys.hcmuns.edu.vn

Abstract: The Đồng Tranh River, the longest of main rivers in Cần Giờ Mangrove Biosphere Reserve, connects the mangrove forests to the East Việt Nam Sea. In recent years, some coastal mangrove areas at the Đồng Tranh estuary are being eroded seriously. Waves, tidal currents, rainfall or river flow changes have been considered as the main reasons for the erosion in this area. In this study, the wave field of the studied area at the Đồng Tranh estuary is computed by using the wave refraction mode. The model is based on the irrotationality of wave number and conservation of the wave action. The model includes wave-current interaction and energy dissipation due to wave breaking in tidal, shallow-water zone. Based on the data of mean wave characteristics, mean currents and real bathymetry at the observed area, the calculated results of the wave field distribution at the Đồng Tranh estuary are given. The change of wave fields depends strongly on initial wave characteristics, currents and water depth of the observed area. They also prove that, the concentration of high wave energy in some sites could be considered as the main cause of erosion in surrounding mangrove areas, especially at Nang Hai mangrove forest. The results also indicate that the model provides a realistic solutions in many practical problems, when some sophisticated models are not available.

I. INTRODUCTION

The Đồng Tranh River, with a length of 67.50 km, is the longest of main rivers in the Cần Giờ District, south of Hồ Chí Minh City. Many studies have been proving that the dynamic processes in this river, as well as the sedimentation and erosion mechanism in its mouth zone, are complicated and changeable. The changes are presumably caused by various natural conditions, such as sedimentary changes, changes of wave propagation, tidal currents, rainfall or river flow change, and by human impact, such as development of shrimp ponds, deforestation [5, 6, 8, 9]. The serious erosion at Nang Hai mangrove area in the Đồng Tranh estuary has been proved as due to wave action [8]. However, up to now the wave field in the Đồng Tranh estuary has not been studied yet. Therefore, this paper aims to calculate the wave field at the Đồng Tranh estuary by using the wave refraction model. This model is based on the irrotationality of wave number and conservation of the wave action. The model includes wave-current interaction and energy dissipation due to wave breaking in tidal, shallow-water zone.

 II. THEORETICAL MODEL FOR WAVE REFRACTION

The refraction model is based on the idea of irrotationality of wave number and conservation of the wave action. The irrotationality of wave number is usually expressed in form of the Snell’s law [2]:

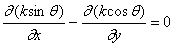               (1)

Where: k is wave number and q: wave direction with respect to the x-axis.

The dynamic part of the problem is described by the conservation of wave action. In order to develop a quantitative model for waves at least on a macroscopic level, the energy dissipation due to wave breaking is included in the equation of the conservation of wave action as follows [4]:

                     (2)

Where: S and W are the x, y components of the wave action;

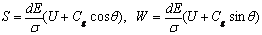                          (3)

Where: the dE is the incremental of wave energy over the wave number band dk and at a directional angle q; the D is wave action dissipation due to wave breaking.

To estimate the dissipated wave action D due to wave breaking, the resemblance between surf zone waves and bores is applied from [3].

The wave motion in the coastal area is induced by wind wave incident from the open sea along the offshore boundary. The mean wave height  and mean wave direction  are assumed to be known along this boundary. A coastal boundary is a moving boundary due to tides. Within the area of interest, the water depth h(x, y) is a varying function of the both coordinates. Moreover, the current velocity vector  is assumed to be known. To avoid the difficulties in defining the boundary condition at the lateral boundaries, outside the area the bottom topography is defined by parallel bottom contours. Unknown functions of the problem are characteristic wave parameters, i.e. 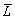significant wave height Hs, mean wave length   and mean wave direction 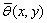in the grid points.

For the arbitrary bottom configuration, the equations (1) and (2) can be solved only numerically. In this study, the finite-difference scheme suggested by Dalrymple [1] is used. In this case, a central difference in x and averaged forward and backward differences in y provides for an O (Dx2, DxDy, Dy2) error.

III. CALCULATIONS OF WAVE FIELD AT THE ĐỒNG TRANH ESTUARY

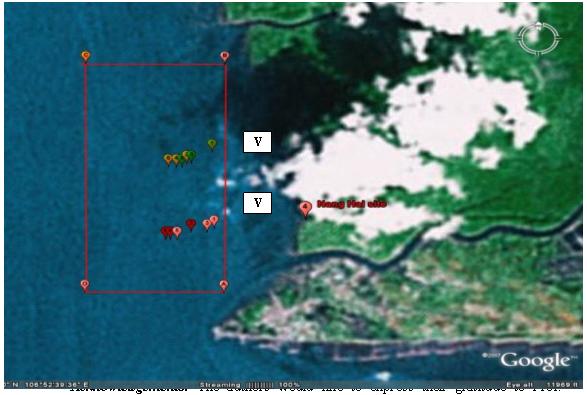
1. Location of the studied site:

The studied arrea is situated at the Đồng Tranh estuary, Cần Giờ District, south of Hồ Chí Minh City. The Cần Giờ District lies in a recently formed, soft, silty delta with an irregular, semi-diurnal tidal regime. The Đồng Tranh is a calm area except for the eastern side near the Đồng Tranh estuary, from the Đồng Hoa River to the Khe Đôi creek. The Đồng Tranh area is less affected by strong wind-induced waves as it is sheltered by the Lý Nhơn and Long Hòa Capes, either side of the estuary. These capes show a trend to be extended due to the alluvial deposition process. As a result, wave propagation into the Đồng Tranh River can change direction from time to time and high waves do not propagate into its estuary all year round. Only winds from the SE to SSW can create direct waves propagation to Đồng Tranh. During the northeast monsoon with easterly disturbance, waves propagation to Đồng Tranh become high, especially for ENE-ESE wind. The waves in Đồng Tranh estuary are also strong, if there is some wind from the SE, SSE or S,  in the transitional season from April to early May. The southwestern monsoon can not create high waves in the Đồng Tranh estuary, except for the case when there is a tropical storm generating SE wind in summer near the offshore of South Việt Nam [7].

2. Dimension of chosen area and initial input data:

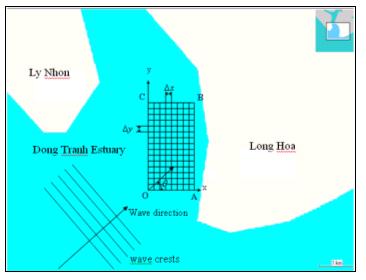
The selected area for wave field calculation is from the Đồng Hoa River to the Khe Đôi creek. The coordinate system O(x,y,z) and the calculated grid OABC are chosen as shown in Fig. 1. The  dimension of the area is about 1300×870 m, with the grid space of  .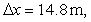

The geographical positions of calculated area OABC are as follows: O = 10o22’50” N, 106o52’4.6” E; A = 10o22’49.8” N, 106o52’33.56” E; B = 10o23’49.2” N, 106o52’34” E; C = 10o23’49.2” N, 106o52’4.6” E. Based on the measured data on the Đồng Tranh River [7], the initial conditions for wave characteristics are chosen as follows: wave period T = 3s, wave direction q = 45°, mean velocity 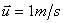 in the NE direction over the observed area. The initial wave height will be chosen in two cases: mean wave height (H0 = 0.5 m) and high wave height (H0 = 1 m).

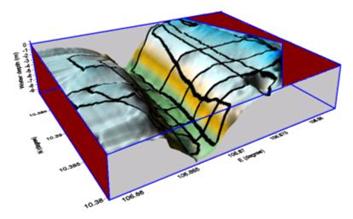
The topography at the Đồng Tranh River was measured in 2008, as shown in Fig. 2. Because of tide on the Đồng Tranh River is rather high, about 2-4 m, the water level should be chosen so that the water level at the muddy flat in front of the sea-mangrove boundary must be high enough for model calculation. The height difference between the muddy flat and the deepest site of the Đồng Tranh estuary is about 10 m. Three cases for high-, medium- and low-water levels have been considered. Consequently, the water levels at the muddy flat can get 1.5, 1.0 and 0.5 m.

IV. COMPUTED RESULTS OF WAVE FIELD AT THE ĐỒNG TRANH ESTUARY

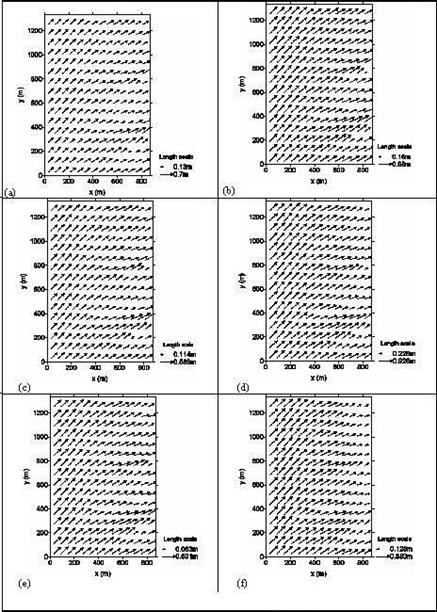
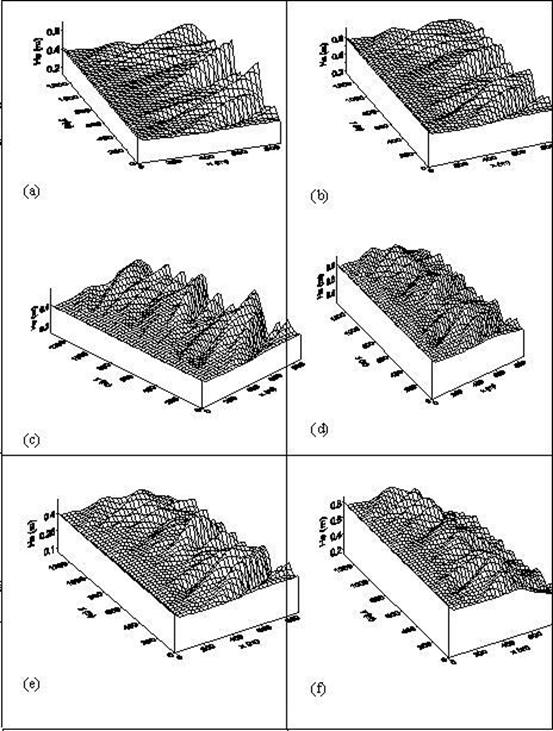
The Fig. 3 and 4 show the computed results of wave fields (Fig. 3) and of significant wave heights (Fig. 4) when the water levels are high (a, b), medium (c, d) and low (e, f) and when initial wave heights get 0.5 m (a, c, e) and 1 m (b, d, f). It is obvious that the waves get refracted and transformed as propagating into shallower area. The wave directions change as they travel from the estuary to shallower water. The approaching angles decrease and the wave crests tend to conform to the bottom contours. Results of q(x, y) calculation are relevant to Snell’s law. The wave height at any particular point depends on two basic mechanisms, i.e. wave shoaling and energy dissipation. At relatively great water depth, the wave shoaling dominates and wave height is increasing. When the limiting water depth is reached, the waves start to be broken and wave height decreases. When the water levels are high and medium (cases a, b, c), most of wave heights increase and the waves are not broken. However, when the water level is low enough (cases e, f) or the initial wave height is high enough (case d), the breaking waves can be observed. Especially in the case f, when the water level is low as well as the initial wave is high, most of waves are broken and the wave height decreases quickly. It is obvious that the wave field depends strongly on initial wave characteristics, currents and water depth of the observed area.

From the computed results of wave field at the Đồng Tranh estuary in six different cases, it should be noted that many highest wave heights concentrate mainly in two special sites, namely X and Y as shown in Fig. 5. In the area X, the highest waves are found in all six cases while in the area Y, the highest waves can be seen only in case of low water. In the Fig. 5, it can be seen that the area X is not far from the Nang Hai mangrove forest. The Nang Hai area is being eroded seriously and quickly, proving that wave action is the main reason for such erosion [7, 8]. Therefore, the calculated results for the concentration of high-wave energy in the area X can be explained and emphasized that wave energy is one of the most important reason of the serious erosion at Nang Hai site.

Figure 1. The calculated area and chosen coordinate system at the Đồng Tranh estuary.

Figure 2. Topography of the Đồng Tranh river area in 2008.

V. CONCLUSIONS

Based on the data of mean wave characteristics and topography at the observed area, the calculated results present the distribution of wave field at the Đồng Tranh estuary. The wave field depends strongly on initial wave characteristics, currents and water depth of the observed area. They also prove the concentration of high wave energy in some sites in calculated area that could be considered as the cause for erosion in surrounding mangrove areas, especially at Nang Hai mangrove forest. The model has some restrictions, such as mean currents, neglect of the energy dissipation due to bottom friction, diffraction… However, the model provides a convenient tool for prediction of wind wave propagation in shallow waters and also provides a realistic solutions in many practical problems, when some sophisticated models are not available.

Figure 3. Computed wave fields when water levels are high (a, b), medium (c, d) and low (e, f) and when initial wave heights reach 0.5 (a, c, e) and 1 m (b, d, f).

Figure 4. Computed significant wave heights when water levels are high (a, b), medium (c, d) and low (e, f) and when initial wave heights get 0.5 (a, c, e) and 1 m (b, d, f).

Figure 5. Concentration of the highest wave energy in the areas X and Y
 at the Đồng Tranh estuary.

Acknowledgements: The authors would like to express their gratitude to Prof. Massel S.R. and Prof. La T. Cang for invaluable advices in the development of the wave model.

REFERENCES

1. Dalrymple R.A., 1988. Model for refraction of water waves. J. of Waterway, Port., Coastal and Ocean. Eng., 114/4 : 423-435. ASCE.

2. Massel S.R., 1989. Hydrodynamics of coastal zones. Elsevier Sci. Publ. Comp., Amsterdam.

3. Massel S.R., Belberova D.Z., 1990. Parameterization of the dissipation mechanism in the surface waves induced by wind. Arch. Mech., 42 : 515-530.

4. Massel S.R., Naguszewski A., 1991. Model for refraction and dissipation of water waves. Proc. Conf. Coastal and Ocean. Eng., 129-134.

5. Mazda Y., Magi M., Nanao H., Kogo M., Miyagi T., Kanazawa N., Kobashi D., 2002. Coastal erosion due to long-term human impact on mangrove forests. Wetl. Ecol. and Manag., 10 : 1-9.

6. Victor S., Neth L., Golbuu Y., Wolanski E., Richmond R.H., 2006. Sedimentation in mangroves and coral reefs in a wet tropical island, Pohnei, Micronesia. Est., Coast. and Shelf Sci., 66 : 409-416.

7. Vo Luong Hong Phuoc, 2006.  Surface waves propagation in mangrove forest and induced suspended sediment concentration. PhD. Thesis, Inst. of Ocean., Sopot, Poland.

7. Vo Luong H.P., Massel S.R., 2006. Experiments on wave motion and suspended sediment concentration at Nang Hai, Cần Giờ mangrove forest, Southern Vietnam. Oceanologia, 48/1 : 23-40.

9. Wolanski E., Mazda Y., Ridd P., 1992. Mangrove hydrodynamics. In Robertson A.I., Alongi D.M. (Eds). Tropical mangrove ecosystems. Amer. Geoph. Union, Washington, 43-62.