I. INTRODUCTION
Mangrove forests are
densely vegetated mudflats that exist at the boundary of marine and terrestrial
environments. Erosion processes on cohesive shores are distinctly different
from those on sandy shores. The eroded fine sediments (silt and clay) are winnowed,
carried offshore, and deposited in deep water in contrast to the sand fraction,
which usually remains in the littoral zone. Furthermore, cohesive sediments are
not transported as bed load, except in the form of fluid mud. They almost
always are transported in suspension form. Therefore in this study, we focus on
the suspended sediment concentration, rather than on the sediment transport.
Hydrodynamic studies in
mangrove forests show that rainfall, riverine flows, tidal currents and waves
are the main causes of suspended sediment transport [1-3, 5, 9, 12]. In
general, the suspended sediment concentration (SSC) near the bottom is much
higher than SSC on the surface due to higher turbulence at the bottom.
Therefore, a 1-D model of vertical profile of sediment suspension is
considered, in which the role of tidal currents and waves are taken into
account. The measured data of SSC in 2004 and 2005 at Nàng Hai area, Cần Giờ
Mangrove Biosphere Reserve, Hồ Chí Minh
II. SUSPENDED SEDIMENT PROFILES AND LOAD TRANSPORT IN MANGROVE FORESTS
In order to determine the SSC profile when it
is not homologous from the bottom to the surface, we use the simple 1-D model
of vertical suspended sediment profile [4, 6]. Within a water column of depth h, the vertical sediment transport is
governed by upward mass diffusion due to turbulence and particulate settling.
The change of concentration C with
time at any elevation, z (measured
positively upward from the mean water level), is determined by the magnitude
and direction of the net sediment flux due to diffusion and settling. The
vertical settling-diffusion equation can be expressed as a particular case of
the general mass conservative equation:
(1)
The equation (1) can be solved for some
initial condition, C(z,0), and
surface (z = 0) and bottom boundary (z = -h) conditions, provided Ws and Kz are specified as shown in the next section.
The boundary condition at the water surface
is that the net flux of sediment at z=0
is nil, i.e.
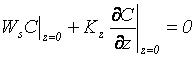(2)
and at the water-fluid mud interface (z = -h) the net flux of sediment is
determined by sediment entrainment, E,
and deposition, S, i.e.
(3)
Specification of the fluxes, E and S, is crucial to an accurate simulation of the suspended sediment
profile.
In the governing equation (1), the unknown
concentration, C, is a function of
the independent variable z and time t. The simplest approach is to
represent function C as a product of
functions Cz(z) and T(t), each depending on variable x and t, respectively, i.e.
(4)
After some calculations, we
can get an expression for vertical concentration Cz(z) in the following form:
(5)
Equation (5) is the linear
second-order differential equation with the boundary conditions 
, in
which Cs and Cb are the concentrations at
the surface and at the bottom. The differential equation (5) can be
approximated by a finite difference equation and becomes a system of matrix
equations. To solve this equation, the Cholesky’s method for a tridiagonal band
type matrix is well suited.
III. SETTLING VELOCITY OF SUSPENDED SEDIMENTS AND DIFFUSION COEFFICIENTS DUE TO WAVES AND CURRENTS
1. Settling velocity
In mangrove forests, the sediment particles
carried in suspension during tidal inundation are cohesive, mainly clay and
fine silt, and form large flocs [2]. The observed exponential decrease in
sedimentation rate with distance from the creek enables the estimation of the
settling velocity Ws of the suspended sediment in mangroves [3]. Assuming zero
re-suspension, the settling velocity Ws can be calculated from
the equation for conservation of sediment mass as follows:
(6)
Where C is the suspended-sediment
concentration, x is the
distance across the mangrove forrest, h is the water depth and U is the current velocity.
2.
Diffusion coefficients due to waves and currents
Various researchers have
tried to model the suspension process by introducing an effective diffusion
coefficient according to specific scenarios such as: suspended sediment induced
by currents for steady flow or for non-steady (tidal) flow, suspended sediment
induced by non-breaking waves, breaking waves or ripples, and suspended
sediment induced by wave and current combination.
Most expressions for the
diffusion coefficient are empirical or semi-empirical. The corresponding
expressions are presented in more detail in Van Rijn [7, 8]. In this study, for
modelling of the suspended sediment concentration, the following diffusion
coefficient is used [4, 6]:
(7)
Where
is the Monin-Obukov
correction for stratification; K0 is the diffusivity under non-stratified or
neutral flow conditions.
For simulating the
influence of stratification under wave motion and for sediment-induced
stratification under tidal current, takes the form:
(8)
In which 
and 
are coefficients depending
on the effect of suspended sediment on the turbulent mixing length; Ri(z) is the gradient
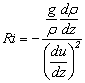(9)
Where ρ is the fluid density; g
- gravitational acceleration; and u(z)
- horizontal velocity.
To simulate enhanced
diffusion for the combined effect of waves and current, Li and Parchure [4]
introduced the following linear form of the diffusion coefficients:
(10)
In which the wave and
current diffusions Kow
and Koc respectively
must be specified, as well as the corresponding weighting coefficients αw and αc. In particular, the diffusion coefficient for wave
motion only is:
(11)
In which h is water depth from the surface; z - vertical coordinate, directed
upward; ω - angular wave frequency; A - wave amplitude; k - wave number; and α0w
- diffusion scaling coefficient, which for a given sediment depends on the flow
field.
On the other hand, the
diffusion coefficient for the current-induced boundary layer is given by:
(12)
Where κ is the von Karman
constant = 0.4; 
- mean current velocity; and n - Manning friction coefficient. The
Manning friction coefficient n is an
important parameter and is the focus of extensive studies on rivers and
channels. This coefficient can be expressed in MKS units, as follows [2, 13]:
(13)
Where I is the gradient of
water surface; and h - water depth.
When sediment concentration
profiles are known, the mixing coefficient can be computed by a simple relationship
[7]:
(14)
However, this equation
cannot be applied when concentrations in the water layer are well mixed due to
high turbulence, especially for strong wave action, in very shallow water in
mangroves.
IV. SSC DATA AND MODEL APPLICATION IN
1. Location of the studied site
Nàng
Hai area is chosen as the studied site. It is about 2.0 km far from the estuary
of the Đồng Tranh river, which with a length of 67.50 km is the longest of the
main rivers in Cần Giờ Mangrove Biosphere Reserve. The Đồng Tranh area is less
affected by strong wind-induced waves as it is sheltered by Capes Lý Nhơn and
Long Hòa, either side of the estuary. The selected chosen site has a more
direct influence on wave motion and the instrumentation transect (10023.427
N; 106052.761 E – 10023.442 N, 106052.793 E)
was chosen parallel to the direction of wave propagation towards the forest.
Nàng Hai is a complicated site with many surrounding creeks and mixed-type
mangroves. Especially, the topography of this site changes remarkably between
muddy flat and mangrove area and being eroded seriously.
Two
field trips in April-May 2004 and January-February 2005 were made at Nàng Hai
area. The aim of the field measurements was to study the influence of wave
motion in mangrove forests and induced sediment concentrations. Data collection
methodology and analysis results were described by [10, 11].
2. Parameters of suspended sediments
From the SSC analysis and calculations, the
final parameters of the suspended sediments at the Nàng Hai site can be
estimated as follows:
- Suspended sediment settling velocity W: - For
tidal currents and weak waves, Ws ≈2.0 - 4.5×10-4
m/s; - For strong waves, Ws ≈2.0 x10-3 m/s.
- Manning friction coefficient
n: - The
mean values, n ≈ 0.016 - 0.021 in MKS
units; - For highest spring tides n ≈ 0.030 in MKS units.
- Diffusion coefficient
Kz: The mean value, Kz ≈ 2.46×10-4
m2/s; - For tidal currents, Kz
≈ 3.35×10-4 m2/s; - For strong waves, Kz ≈ 1.18×10-3 m2/s.
It is noticeable that these parameters are
calculated to estimate the general characteristics of the Nàng Hai studied site
and to be applied in the 1D model of vertical suspended sediment profile.
3.
Calculated results of vertical suspended sediment concentrations
When the SSC is not homogeneous, the 1-D
model of vertical suspended sediment transport can be applied to determine the
SSC profile. When the suspended sediment profile C(z) at a given point is determined, the total SSC Ctol during a tidal cycle can
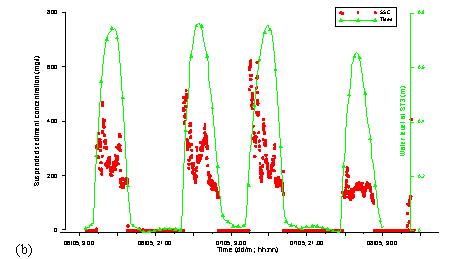
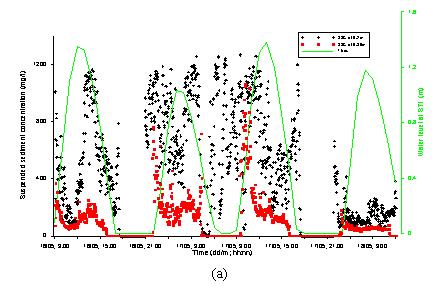
be calculated. The calculated results of SSCs during one tidal cycle were
considered under three different cases of weather conditions: influence of
tidal current, under high waves and influence of tropical low pressure.
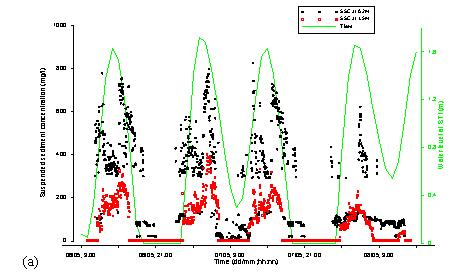
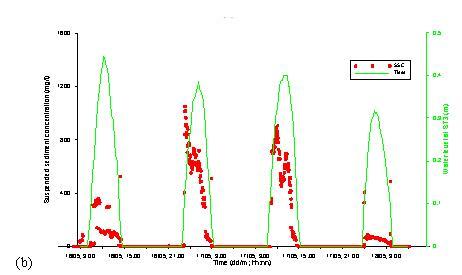
The field measurement of
SSC on 19-20 April 2004 was carried out in calm weather with weak wind and calm
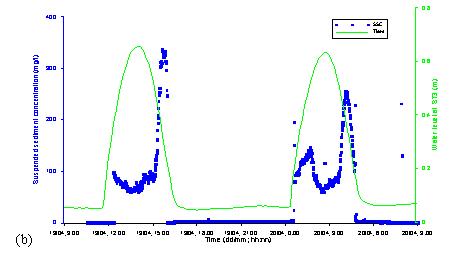
sea. Figs. 1a, b show the changes of SSC at stations ST1 and ST3, respectively.
The station ST1 is deployed in the muddy flat 20 m before the mangrove front
and the station ST3 is 45 m within the mangroves. It is obvious that the
changes of SSCs depend mainly on tidal level; the SSCs are higher during the
ebb and the flow tide, but decrease at the slack tide when the tidal current is
almost zero. Fig. 1a shows SSC at ST1 at three different levels, namely:
near-bottom, middle and top levels. It is obvious that SSC near the bottom is
much higher and fluctuates more than SSC in the middle and near-surface levels.
Inside the mangroves at ST3, the concentration changes also due to tidal level
and has lower values than at the muddy flat station ST1, namely 50 mg/l at
slack tide and about 100 mg/l at flow and ebb (Fig. 1b). The lower
concentration at ST3 in the mangroves suggests that mangrove vegetation can
encourage the retention of sediment.
It is known that flow currents flow toward
the coast during flow phase and ebb currents go away from the coast. Therefore,
the concentrations can be considered as positive for towards mangrove flow and
as values for seaward flow.
The total concentration is the difference
between concentrations for flow tide and for ebb tide. From the calculation, it
can be seen that the concentrations at ebb tide Cebb are higher than those at flow tide Cflow at two stations.
Especially at ST1, concentration Cebb
is much higher than concentration Cflow.
As a result, the total concentrations Ctol
at theses stations have negative values. The negative value of SSC suggests
that more sediment tends to move seaward. This can encourage erosion at these
locations, particularly of the mangrove front at ST1.
