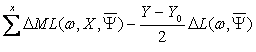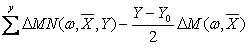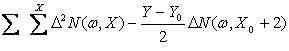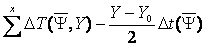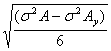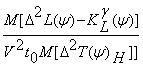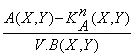THEORETICAL BASIS OF METHOD
OF SEISMIC OBSERVATION GROUPING (SOG)
TRƯƠNG MINH
Việt Nam Association of Geophysicists,
Hà Nội
Abstract: The method of seismic observation grouping
(SOG) puts forward the dynamic and kinematic
solutions which divide the surface and depth factories depending on the seismic
rays formed as two-ray, four-ray and six-ray groupings.
This method
has the following aims:
- To estimate the errors of dynamic and
kinematic measures in seismic exploration;
- To estimate dynamic and kinematic
(static) corrections;
- To study on changes of characteristics
of reflection horizon;
- To study the characteristics of velocity
and attenuation of transmission media.
I. INTRODUCTION
To day, the seismic exploration involves handling
complex tasks in the study on geology, especially in the search for and
exploration of petroleum. The practical needs require that the information
available in the seismic data makes the best use in order to improve the
accuracy to define physical parameters of the geological media. To satisfy this
requirement, a number of factors which deform the characteristics of wavelet,
including those of emission, transmission media and wave receiving point must
be overcome. Important task is to extract the impact of these characteristics
from the observable seismic signal in order to study and assess them. By this
way we can define the correction of surface condition and study on
characteristics of the media. In case of identical media, we temporarily put
aside the impact of the characteristics of transmission, attenuation and
separation of reflection wave in the media between emissions and receiving
point, the complex spectra of reflection seismic wave can be described as
follow:
S(w, X, Y, Y) = m(w,X) .l (w, Y). n (w,Y). (1)
This shows the interdependence of the
characteristics of complex spectra of the emission m(w,X), reflection l(w,Y) and reception n(w,Y) areas; w is frequency of
reflection wave, X, Y, Y are coordinates of shot point, reflection point and receiving point.
In the time domain, the signal of reflection wave
is illustrated as follows:
ŋ(t,X, Y, Y) = 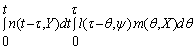 (2)
(2)
The time for transmission of reflection as defined
as follows:
T(X, Y, Y) = t(X) + t(Y) + t(Y) + t(X,Y) (3)
In which t(X), t(Y), t(Y) are transmission times
at these zones of emission receiving, reflection and reception, t(X,Y)
is the time of transmission in the seismic media.
Based on the acknowledgement of the model of the
above mentioned media, the task to be solved is to extract the impact of the
surface and depth conditions to study on changes of their dynamic and kinematic
characteristics along the observation line.
II. METHOD OF GROUPING FOR COMMON SHOT POINT (CSP),
COMMON DEEP POINT (CDP) AND COMMON RECEIVING POINT (CRP)
By gathering observation of reflection wave
according to CSP, CDP & CRP, the quality of change of the surface and depth
conditions can be assessed along the study line.
Suppose that at the two common reflection points Ψ1
and Ψ2 we observe signal S1 and S2 and in
order to discover the change in the characteristics of their reflection, we
assume coincidence or none coincidence of characteristics of the two reflection
points Ψ1 and Ψ2 owing to criteria Fisher.
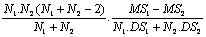 < F (4)
< F (4)
Iin which: N1 and N2 are
observation folds of CDP for each common deep point at the position of Ψ1
and Ψ2; MS and DS are mathematical expectance and dispersion
respectively for the complex spectra at these two points.
Beyond the criteria F, we can conclude that the
changes in the characteristics of reflection between these two points are
conservable anomaly. Similarly for the common shot points and the common
receiving points we can use criteria (4) to assess the change of surface
conditions.
In the time domain we can use criteria Student.
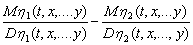 < S (5)
< S (5)
In which: Mŋ and Dŋ are mathematical expectance and dispersion of seismic waves.
III. SPECIAL SEISMIC OBSERVATION GROUPINGS
Based on the seismic observation groupings for
shot, we can achieve the dynamic and kinematic solution which divides the
surface and depth factory depending on the seismic rays to be formed as so
called the two-ray, the four-ray and the six-ray groupings.
1. Two-ray seismic grouping
To illustrate this, we mark a seismic observation
ray as [X, Ψ, X], where X, Ψ, Y are coordinates of emission, reflection and
receiving points (see Fig. 1-3).
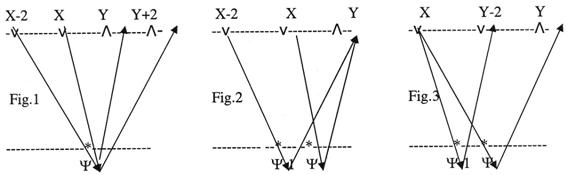
a. Definition of spectral
characteristics of emission, reflection and receiving areas.
We mark the differential of the characteristics at
two emission points in the group [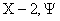 ,
, 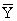 -2] and [
-2] and [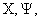
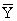 ] with fixed coordinate
] with fixed coordinate 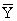 (Fig. 1), as follows:
(Fig. 1), as follows:
DMN (w, X, 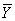 ) = ln
) = ln (6)
(6)
In the group [ ] and [
] and [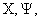
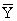 ] with fixed
] with fixed  (Fig. 2):
(Fig. 2):
DML (w, X,  ) = ln
) = ln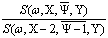 (7)
(7)
The differential of the characteristics at two
refection points in group [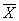 ,
,
 ] and [
] and [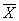 -2,
-2,  -1,
-1, ] in fixed coordinate
] in fixed coordinate 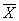 (Fig. 2), as follows:
(Fig. 2), as follows:
DLM (w,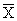 ,
, ) = ln
) = ln (8)
(8)
With the fixed 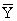 (Fig. 3):
(Fig. 3):
DLN (w, ,
,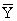 ) = ln
) = ln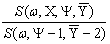 (9)
(9)
The differential of the characteristics at two
receiving points in group [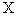 ,
, ,
, ] and [
] and [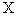 ,
,  -1,
-1,  -2] with the fixed coordinate
-2] with the fixed coordinate (Fig. 3), as follows:
(Fig. 3), as follows:
DNL (w, ,
,  ) = ln
) = ln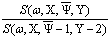 (10)
(10)
With the fixed  (Fig. 3):
(Fig. 3):
DNM (w, ,
, ) = ln
) = ln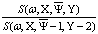 (11)
(11)
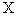 = Y = 2, 4....coordinate of the
emission point;
= Y = 2, 4....coordinate of the
emission point;  = 1, 2 ....coordinate of the reflection points;
= 1, 2 ....coordinate of the reflection points; 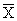 ,
,
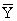 ~ fixed coordinates of
the emission, receiving and reflection points.
~ fixed coordinates of
the emission, receiving and reflection points.
b.
Definition of the spectral characteristics of emission, reflection and receiving
of reflection wave along lines.
Emission spectral characteristics:
m(w,x)=Exp[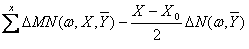 ] (12)
] (12)
=Exp[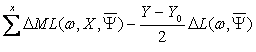 ] (13)
] (13)
Receiving spectral characteristics:
n(w,Y)
= Exp [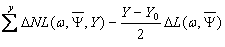 ] (14)
] (14)
= Exp [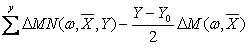 ] (15)
] (15)
Reflection spectral characteristics:
l(w, Y) = Exp [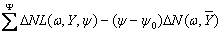 ] (16)
] (16)
= Exp[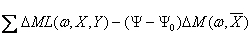 ] (17)
] (17)
The values of ΔM(w,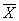 ), DN(w,
), DN(w,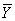 ), DL(w,
), DL(w, ) for the fixed coordinates
) for the fixed coordinates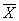 ,
, 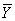 and
and  are defined as angle coefficient
of the functions ΣΔMN, ΣΔNL, ΣΔML, in the equations (9)-(14).
are defined as angle coefficient
of the functions ΣΔMN, ΣΔNL, ΣΔML, in the equations (9)-(14).
The values of m(w, X), n(w,Y) and l(w, Y) define the complex
characteristics of emission, receiving and reflection zone compared to their
original values (X0, Y0, X0).
Therefore, we can extract them to study frequency characteristics at the
emission, receiving and reflection point independently along the observation
line.
2. Four-ray seismic observation grouping SOG4.
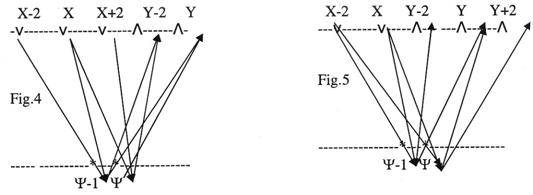
For the group of rays [X-2, Y-1, Y], [X, Y, Y], (X, Y-1, Y-2], [X+2, Y, Y-2] (Fig. 4), the
second differential of spectral characteristics of the emission area is defined
as follows:
D2M(w,x)= ln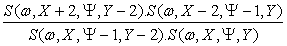 (18)
(18)
For the group of rays [X-2, Y-1, Y], [X-2, Y, Y+2], [X, Y, Y], [X, Y-1, Y) (Fig. 5), the
second differential of the spectral characteristics of the receiving area:
D2N(w,Y)= ln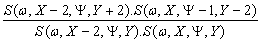 (19)
(19)
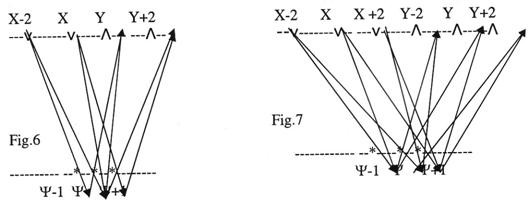
For the group [X-2, Y-1, Y], [X-2, Y, Y+2], (X, Y, Y] and [X, Y+1, Y] (Fig. 6), the
second differential of the spectral characteristics of the reflection
area:
D2L(w, )= ln
)= ln (20)
(20)
The spectral characteristic variation of emission
m(w,x),
receiving n(w,y) and reflection l(w,Y) along observed line are defined as follows:
M(w,x)=Exp[ ] (21)
] (21)
N(w,y)=Exp[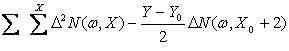 ] (22)
] (22)
L(w,Y)=Exp [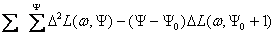 ] (23)
] (23)
The values of DM (w, X0+2), DN (w, Y0+2) are
defined as angle coefficient of the function SSD2M (w, X), SSD2N (w, Y), SSD2L (w, Y) in the equations (21),
(22) and (23).
Therefore with the characteristics of m (w, x), l (w, Y) and n (w, y) we can study the
spectral characteristics of emission, reflection and receiving independently by
extracting each other impact along the observation line.
3. Definition of kinematic characteristics.
a. For two-ray grouping:
Handling a kinematic analysis is similar to that of
dynamic task one based on the equation (3). In case of ideal media if the
sloping of reflection surface is not big and after the correction NMO, the
values of t(x, y) in the equation (3) are immutable based on the two-ray
grouping.
We have the first differentials of the kinematics
characteristics at two emission points in the group [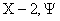 ,
, 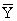 -2] and [
-2] and [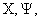
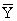 ] with fixed
] with fixed 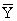 , as follows:
, as follows:
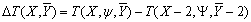 (24)
(24)
Difference of the kinematic characteristics at two
refraction areas  :
:
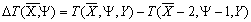 (25)
(25)
Difference of the kinematic characteristics at two
receiving areas Y:
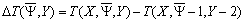 (26)
(26)
Transmission time of wave in the emission area X:
t(x) = 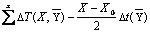 (27)
(27)
= 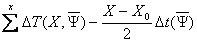 (28)
(28)
Transmission time of wave in
receiving area Y:
t(y) = 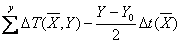 (29)
(29)
= 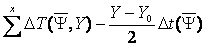 (30)
(30)
Transmission time of wave in reflection area:
t(Y) = 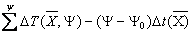 (31)
(31)
= 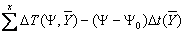 (32)
(32)
The values of Δt (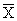 ), Δt (
), Δt (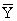 ), Δt (
), Δt ( ) are defined as angle
coefficient of the functions t(x), t(y) and t (Y) in the equations (27) -
(32)
) are defined as angle
coefficient of the functions t(x), t(y) and t (Y) in the equations (27) -
(32)
b. For four-ray grouping:
The second differentials of the kinematics
characteristics at the emission, refraction and receiving areas are as follows:
D2T(x) = T(X+2, Y, Y-2) + T(X-2,Y-1,Y) - T(X, Y-1, Y-2) - T(X, Y, Y) (33)
D2T(Y) = T(X, Y+1, Y+2) + T(X-2,Y-1,Y) - T(X, Y, Y) - T(X-2, Y, Y+2) (34)
D2T(y) = T(X-2, Y, Y+2) + T(X,Y-1,Y-2) - T(X-2, Y-1, Y) - T(X, Y, Y) (35)
The time characteristics of the emission t(x)
receiving point's t(y) and the reflection surface t (Y) are defined as follows:
t(x)= 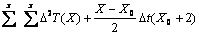 (36)
(36)
t(Y)= 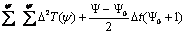 (37)
(37)
t(Y) =  (38)
(38)
The values of Δt(X0+2),
Δt(Y0+1), Δt(Y0+2) are
defined as angle coefficient of the functions t(x), t(Y) and t(y) in the
equations (36) - (38)
The values of t(x), t(y) are those of static
corrections for emission and receiving conditions. And t(Y) is time variation of the
reflection surface.
4. Criteria for controlling the dynamic and
kinematic measurements of reflection wave
Based on the six-ray
seismic grouping (see Fig. 7) [X-2, Y-1, Y], [X-2, Y, Y+2), [X, Y +1, Y+2], [X+2, Y, Y-2) [X+2, Y+1, Y], in the frequency
domain we have correlations:
A (w, X, Y) = ln 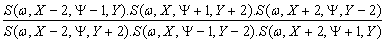 = 0 (39)
= 0 (39)
And in the time domain:
B(x,y) = T(X-2, Y-1, Y) + T(X, Y+1, Y+2) + T(X+2, Y, Y-2) -
- T(X-2, Y, Y+2) - T(X, Y -1, Y - 2) - T(X+2, Y+1, Y) = 0 (40)
While observing random noises, the characteristics
of distribution and evil of their impact on the measurement values show that if
there is regular wave interference the normal distribution of amplitude will be
broken, the multiplicative and additional noise will have an impact on the
distribution of amplitude in one way or the other. The additional noise is
basically in the kinematic measurement.
It is necessary to estimate the values of
systematic deformation by the impact of wave attenuation and divergence, the
velocity of seismic wave and overlying formation, the anisotropic
characteristics of source and the receiver on the first and second differential
of the characteristics of the emission, receiving and reflection areas and the
criteria for observation examination. To pay attention to that the level of
distortion depends mainly on the emission interval l over the depth h of the
reflection surface (L =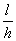 ) when L > 0.1 then the errors will be small and can be overlooked.
Results of the theoretical estimates have laid the basis for the selection of
the best parameters for seismic observation system in the method of seismic
observation grouping.
) when L > 0.1 then the errors will be small and can be overlooked.
Results of the theoretical estimates have laid the basis for the selection of
the best parameters for seismic observation system in the method of seismic
observation grouping.
When the criteria for examining dynamic measurement
A (w, x,
y) ¹ and
kinematic measurement B (x, y) ¹ 0, a set of noise and errors through the
process of measuring signal will be shown.
On the basic of the six-ray grouping, the errors of
the measurement dynamic and kinematic values can be estimated.
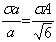 ;
; 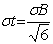 (41)
(41)
In which: σa and σt are the errors of separate measured values of the amplitude and
time for reflection wave, σA and σB are mean square errors of the values
of A(w, X,
Y) and B(X, Y).
The SOG method can also estimate the errors of the
separate measured values by separate factors:
σam = 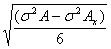 (42)
(42)
σal =  (43)
(43)
σan = 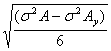 (44)
(44)
σa0 =  (45)
(45)
In which: σam,
σal, σan and σa0 are the errors of separate measured values of the
amplitude caused by the emission, receiving conditions and their unestimatable
factors. σ2Ax,
σ2AY, σ2Ay is dispersion of the
values of A(x, y) at the fixed coordinates X, Y, Y correspondingly. And σA is the common dispersion of the
values of A(x,y) for the whole of measured values. By the similar way will be
able to analyze the errors of kinematic measured value based on the criteria
B(x, y).
5. Study on the
characteristics of attenuation and velocity of
transmission of seismic wave by SOG method
a. Estimation of the effective
attenuation coefficient
The estimation shows that the deviational values by
SOG method will increase corresponding to L parameters, when L > 0.3 it is
necessary to consider their effect in the data processing when using deviation
effect of the second differential values D2 and the criteria for the
examination A and B, the attenuation coefficient and velocity of seismic wave
in the overlying formation can be estimated.
aef = -2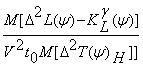 (46)
(46)
The effective attenuation coefficient comes also to
be found by the six-ray grouping as follows:
aef = 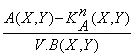 (47)
(47)
To estimate the effective velocity:
Vef =  (48)
(48)
In which: l
is emission interval; M [D2T (Y)H)] - the mathematical expectance of second differential of the transmission
time at the reflection point Y; D2T(Y)H - the second
differential of transmission time of
reflection wave in the reflection zone Y; M[D2L(Y)H) - the mathematical expectance of the values of D2L(Y); D2L (Y)H - the second differential values of dynamic characteristics of the
reflection at point Y; K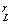 (Y)
- the deviation of the observation values D2L(Y) by wave
diverge; A(x, y) and B(x, y) - the criteria of examining
the amplitude and time; K
(Y)
- the deviation of the observation values D2L(Y) by wave
diverge; A(x, y) and B(x, y) - the criteria of examining
the amplitude and time; K (X, Y) - the deviation values
of A(x, y) by diverge; V - an averaged
velocity.
(X, Y) - the deviation values
of A(x, y) by diverge; V - an averaged
velocity.
b. Experimental results and application of SOG
method in practice
On the basis of SOG algorithms, a set of processing
programs was set up for the purposes:
- Estimating the errors of the dynamic and
kinematic measures.
- Estimating the amplitude and spectra correction
for the surface conditions;
- Setting up the dynamic section;
- Estimating the effective attenuation coefficient;
- Defining the characteristics of reflector;
- Defining the static correction on the surface
condition;
- Defining the effective velocity.
The method SOG has been experimented through
processing seismic data in different areas of Russia
and Việt Nam.
The analysis of the errors of dynamic measured
values in Tiumen (Russia) shows that in a number of cases their distribution
law is almost close to that of normal distribution except for a couple of
special cases which are close to the Jauffret distribution. In any case, the
errors of the measured values will increase normally if the emission interval
increases. Basically, this has something to do with the increase of random
noise level. Analyzing the erroneous factors show that the random noise has
nothing to do with the shot point, but the reflection and receiving points play
an important part in shaping these errors. Through the result of processing we
have achieved the first and second differential values of dynamic
characteristics at the study line, from which we get the values of dynamic
corrections at the shot point, receiving point and the dynamic characteristics
of reflection horizon.
The work of kinematic processing has been carried
out on the seismic data in Astrakhan (Russia).
The study of the distribution of errors for the time of transmitting reflection
wave is close to the normal distribution.
The analysis of amplitude and spectra has been
carried out based on seismic data available in Pricaspian basin. Through the
results of processing we got dynamic correction and sections. The values of
correction by separate method are well linked along the line.
In the Red
River Basin (Việt Nam) the application of SOG method
to study the velocity sections in different areas has brought some successes
which correspond to the drilling data. The analysis of the characteristics of
velocity along the axis of this basin allows us to define horizontally and
vertically the laws of change in velocity of seismic wave which links to the
change of thickness of overlying Neogene formations.
To study the characteristics of the attenuation of
sections we have applied elective attenuation coefficient and the layered
attenuation coefficient to compare these results with the logging data. The
bedded attenuation coefficients are reduced in conformity with the rules once
the depth is extended, while there is a big gap (up to 5.10- m) and
more to the strong boundary.
IV. CONCLUSIONS
According to the SOG method we are able to find a
model of appropriate seismic signal in order to research on a solution to the
extraction of the impact surface and depth conditions to observe them
separately; especially this method has been successfully applied for the study
on dynamic characteristics (amplitude and specters) of reflection seismic
waves.
The successful application of SOG method can help
us to solve the following problems:
1. To estimate the errors of dynamic and kinematic
measures;
2. To estimate dynamic corrections created by wave
emission and receiving conditions;
3. To estimate the static corrections;
4. To study on changes of characteristics of
reflection horizon concerning his structure and lithology composition;
5. To study on the characteristics of attenuation
of transmission media;
6. To study on the velocity characteristics of the
geological section.
The parameters of the media given by the SOG method
will greatly contribute to the prediction of geological sections and in the
direct search for the petroleum.
REFERENCES
1. Gurvich I.I., Truong Minh,
1971. Application of seismic observation grouping to definite the
characteristics of for emission, reflection and reception areas by seismic data. Geology and Exploration, 7. Moscow.
2. Gurvich I.I., Truong Minh,
1972. To evaluate the precision of the dynamic measure-ments by reflection
seismic observation grouping. Geology and
Exploration, 10. Moscow.
3. Trương Minh, 1982. Theory
of seismic observation grouping applied to seismic stratigraphy. Oil and Gas J., 1. Hà Nội.
4. Truong Minh, 1987. Method
of seismic observation grouping for the dynamic and kinematic analyses of the
reflection wave. Dr. Sci. thesis, Nat.
Libr. of SRV., Hà Nội; Nat. Libr. of R.F., Moscow.
![]() (2)
(2)![]() < F (4)
< F (4)![]() < S (5)
< S (5)