PHƯƠNG
PHÁP NGHIÊN CỨU
PHƯƠNG PHÁP GIẢI CHẬP EULER MỞ RỘNG VÀ ỨNG DỤNG TRONG
LUẬN GIẢI SỐ LIỆU DỊ THƯỜNG TỪ THEO TUYẾN
VÕ THANH SƠN
Viện Vật lý địa cầu, Viện KH & CN VN, 18 Hoàng Quốc Việt, Hà Nội
Tóm tắt: Trong bài báo này, chúng tôi trình bày phương
pháp giải chập Euler mở rộng đối với các ranh giới tiếp xúc và đai mỏng để luận
giải số liệu dị thường từ theo tuyến. Cơ sở của phương pháp dựa trên phương
trình đồng nhất Euler của thế từ và biểu thức của nó sau khi đã thực hiện một
phép quay. Phương pháp này có thể áp dụng trực tiếp cho tuyến số liệu dị thường từ
ở vùng vĩ độ thấp mà không cần thông tin về độ từ hoá. Phương pháp giải chập Euler mở rộng đã được thử
nghiệm với mô hình lý thuyết của các ranh giới tiếp xúc, các đai mỏng và cho
kết quả tốt. Hiệu quả của phương pháp được khẳng định bằng việc luận giải tuyến
số liệu dị thường từ hàng không Nam
Định - Hải Phòng nằm ở phía đông nam Hà Nội.
I. MỞ ĐẦU
Việc sử dụng phương pháp giải chập Euler để luận giải
số liệu trường thế (trọng lực và từ) nhằm xác định vị trí và độ sâu của nguồn
đã được áp dụng rất rộng rãi trên thế giới [1, 4, 5, 12, 13, 14, 15]. Lần đầu
tiên vào năm 1982, Thompson đã phát triển kỹ thuật này và áp dụng nó để luận giải
số liệu theo tuyến 2-D [15]. Đến năm 1990, Reid và nnk đã phát triển mở rộng
phương pháp này để luận giải số liệu 3 chiều (3-D) [12]. Hầu hết những phát triển
gần đây về phương pháp này là những kỹ thuật nhằm loại bỏ các nghiệm xấu, ví dụ
như áp dụng một tiêu chuẩn chấp nhận nghiệm dựa theo độ lệch chuẩn trong việc
đánh giá độ sâu [15]; áp dụng bộ lọc Laplace để giới hạn nghiệm [4]; sử dụng vị
trí của đường cong tín hiệu giải tích như là một tiêu chuẩn chấp nhận nghiệm
[5]....
Phương pháp giải chập Euler mở rộng đối với các ranh
giới từ tính và đai mỏng trong không gian hai chiều mới được phát triển gần đây,
năm 2001 [7]. Phương pháp này cũng là một kỹ thuật dùng để loại bỏ các nghiệm
xấu và có thể coi nó là một phương pháp lựa chọn. Những sai số gặp phải khi áp
dụng phương pháp này phụ thuộc vào mức độ của việc loại bỏ những nghiệm xấu và
độ lệch chuẩn. Phương pháp giải chập Euler mở rộng cho phép xác định rất nhanh
vị trí, độ sâu, góc nghiêng và độ tương phản từ cảm của nguồn gây dị thường từ,
mà không cần thông tin về độ từ hoá, và có thể áp dụng trực tiếp cho tuyến số
liệu dị thường từ ở vùng vĩ độ thấp và xích đạo từ. Cơ sở của phương pháp dựa trên tính chất của phương trình đồng nhất
Euler của thế từ và biểu thức của nó sau khi đã thực hiện một phép quay.
Nhìn chung ở Việt Nam,
các phương pháp luận giải số liệu dị thường từ theo tuyến còn ít, nhất là các
phương pháp mới được phát triển gần đây trên thế giới thì việc áp dụng chúng ở
Việt Nam
còn hạn chế. Mới đây, một số tác giả đã áp dụng phương pháp giải chập Werner nhiều
nguồn để luận giải tuyến số liệu dị thường từ và cho kết quả khá tốt [6].
Trong khuôn khổ của bài báo này, chúng tôi sẽ trình
bày phương pháp giải chập Euler mở rộng đối với các mô hình của ranh giới tiếp
xúc, đai mỏng và kết quả áp dụng phương pháp này trong luận giải tuyến số liệu
dị thường từ hàng không Nam Định - Hải Phòng.
II. PHƯƠNG PHÁP
GIẢI CHẬP EULER
MỞ RỘNG
1. Phương trình Euler mở rộng
Xét không
gian 2-D với độ sâu z (hướng dương ở phía dưới) và phương nằm ngang x.
Đối với một loại đặc biệt của dị thường từ, trường thế M là hàm đồng
nhất bậc n của khoảng cách r; ở đây  trong mặt phẳng 2-D; như vậy M
thoả mãn phương trình sau [15]:
trong mặt phẳng 2-D; như vậy M
thoả mãn phương trình sau [15]:
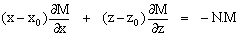 (1)
(1)
Đây là
phương trình Euler 2-D, với N là chỉ số cấu trúc. Nếu chỉ số cấu trúc
của nguồn biết, chúng ta có thể xác định được vị trí và độ sâu của nguồn gây dị
thường.
Khi hàm đồng nhất bất biến dưới phép
quay 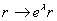 , chúng biến đổi thế
, chúng biến đổi thế 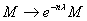 , thì từ sự bất biến này ta có:
, thì từ sự bất biến này ta có:
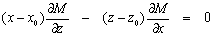 (2)
(2)
Một ví
dụ minh họa là chúng ta xét trường hợp mà trường thế suy giảm theo khoảng cách so
với nguồn, ta có phương trình:
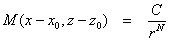 (3)
(3)
ở đây C là một hằng số liên quan với tính chất
vật lý của nguồn và 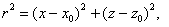 như vậy građien của trường sẽ là:
như vậy građien của trường sẽ là:
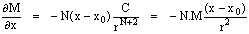 (4)
(4)
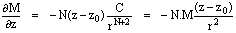 (5)
(5)
Từ
đây, nhân phương trình (4) với (x - x0) và phương
trình (5) với (z - z0) và cộng chúng với nhau, sẽ cho
phương trình đồng nhất Euler (phương trình (1)). Nhân phương trình (4) với (z
- z0) và phương trình (5) với (x - x0)
và trừ chúng với nhau, sẽ cho phương trình của phép quay (phương trình (2)).
2. Ranh giới tiếp xúc từ
tính
Các phương
trình của trường từ (M) và đạo hàm của nó đối với ranh giới tiếp xúc ở
vị trí (x0, z0) và kéo dài theo độ sâu đã
được Nabigian đưa ra [8]. Đối với đạo hàm thẳng đứng và nằm ngang, ta có:
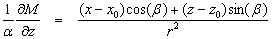 (6)
(6)
và
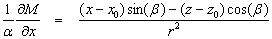 (7)
(7)
ở đây: a = 2KFcsin(d), b=
2I-d-90o cho trường
hợp trường dị thường toàn phần, và 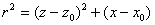 , với K là giá trị độ tương phản từ
cảm của ranh giới tiếp xúc, d là góc nghiêng, F là giá trị trường
toàn phần của Trái đất,
, với K là giá trị độ tương phản từ
cảm của ranh giới tiếp xúc, d là góc nghiêng, F là giá trị trường
toàn phần của Trái đất, 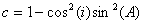 , trong đó i là độ từ khuynh của
môi trường và A là góc giữa phương bắc từ và trục x, và tan(I)
= tan(i)/ cos(A). Thay thế vào các phương trình (1) và (2) ta có:
, trong đó i là độ từ khuynh của
môi trường và A là góc giữa phương bắc từ và trục x, và tan(I)
= tan(i)/ cos(A). Thay thế vào các phương trình (1) và (2) ta có:
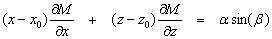 (8)
(8)
và
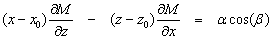 (9)
(9)
Các phương
trình (8) và (9) là sự mở rộng của phương trình Euler đối với ranh giới tiếp
xúc từ, mà về mặt lý thuyết có chỉ số cấu trúc là 0.
Phương
trình (8) đã được Reid và nnk cải tiến [12], họ giải nó với việc coi vế phải
của phương trình như là một tập hợp các hiệu ứng của biên độ, đường phương và
góc nghiêng của vật thể gây dị thường. Bằng sự cải tiến tương tự cho phương
trình (9), các vế phải của 2 phương trình bây giờ cho hai phương trình với 2 ẩn
số; từ đó có thể tìm a và b. Nếu biết giá trị cường độ của trường từ,
độ từ khuynh và độ từ thiên, chúng ta có thể xác định được góc nghiêng và độ tương
phản từ cảm của ranh giới tiếp xúc từ tính với giả thiết không có độ từ dư.
Đầu tiên,
ở mỗi cửa sổ trượt dọc theo tuyến, giải phương trình (8) bằng phương pháp bình
phương tối thiểu để xác định x0
và z0, ký hiệu đs1 = z0 [11]. Tiếp đó giải đồng
thời các phương trình (8), (9) và xác định được các giá trị x0, z0, a, b; ký hiệu đs2 = z0. Sau đó tính tỉ lệ phần trăm của [(đs2-đs1)/đs2] x 100%.
Nếu như tỉ lệ phần trăm nhỏ hơn một ngưỡng nào đó (chẳng hạn như 10%) thì giá
trị đs2 và x0, góc nghiêng, độ tương phản từ cảm tương ứng được
lựa chọn.
3. Đai mỏng
Phương
trình trường từ của một đai mỏng kéo dài theo độ sâu có vị trí tại đỉnh (x0,
z0) là đạo hàm nằm ngang do trường của ranh giới tiếp xúc từ tính
tại vị trí đó gây ra và là phương trình dưới đây [8]:
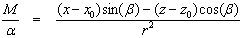 (10)
(10)
với a = 2KFctsin(d), ở đây t
là độ dày của đai. Như vậy, đạo hàm nằm ngang và thẳng đứng của trường dị
thường từ do đai mỏng gây ra sẽ là:
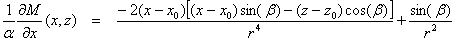 (11)
(11)
và 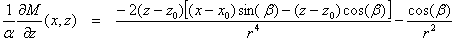 (12)
(12)
Thay thế
chúng vào các phương trình (1) và (2) chúng ta có:
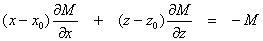 (13)
(13)
và 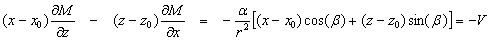 (14)
(14)
Phương
trình (13) là phương trình Euler của đai mỏng với chỉ số cấu trúc là 1. Sự thú vị
ở chỗ là trong phương trình (14), V là građien thẳng đứng của trường từ
của ranh giới tiếp xúc tương đương (phương trình (6)). Từ đó phương trình (13)
được dùng để xác định vị trí trên mặt phẳng nằm ngang và độ sâu của nguồn, tiếp
đó phương trình (14) được sử dụng để xác định V.
Chúng ta
dễ dàng thấy rằng:
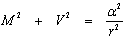 (15)
(15)
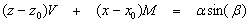 (16)
(16)
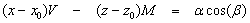 (17)
(17)
Như vậy, góc nghiêng, độ tương phản từ cảm và độ dày
của đai mỏng có thể được xác định, nếu chúng ta biết giá trị cường độ trường từ
và giá trị độ từ khuynh với giả thiết không có độ từ dư. Từ M và V
là giá trị đạo hàm nằm ngang và thẳng đứng do trường của ranh giới tiếp xúc tương
đương với đai mỏng gây ra, các phương trình (16) và (17) cho thấy sự tương tự
các phương trình (8) và (9) (hai phương trình này là sự mở rộng của phương trình
Euler đối với ranh giới tiếp xúc từ tính).
Cách thức tính toán đối với trường hợp đai mỏng cũng
gần giống như ranh giới tiếp xúc. Trong mỗi cửa sổ trượt dọc theo tuyến đo, giải
phương trình (13) để xác định x0,
z0; ký hiệu đs3 = z0. Từ những giá trị x0, z0 này, ta xác định V
bằng phương trình (14). Tiếp đó giải đồng thời phương trình (15), (16) hoặc
(17) để xác định các giá trị a, b. Sau đó,
từ các giá trị M và V (đạo hàm của ranh giới tiếp xúc tương
đương), giải phương trình (8) để xác định x0, z0;
ký hiệu đs4 = z0. Tiếp đó,
tính tỉ lệ phần trăm của [(đs4-đs3)/đs4] x 100%. Cuối cùng, nếu tỉ lệ phần trăm
nhỏ hơn một ngưỡng nào đó (ví dụ 10%) thì các giá trị đs4 và x0,
góc nghiêng, độ tương phản từ cảm tương ứng được lựa chọn.

Hình 1. Trường dị thường
từ, đạo hàm nằm ngang và đạo hàm thẳng đứng
của ranh giới tiếp xúc và đai mỏng riêng biệt.
III. ÁP DỤNG VỚI MÔ HÌNH LÝ THUYẾT
Để làm sáng tỏ khả năng áp dụng phương pháp giải chập
Euler mở rộng, chúng tôi đã tiến hành tính mô hình
trường từ cho các đối tượng sau:
- Ranh giới tiếp xúc từ tính riêng biệt và 4 ranh
giới tiếp xúc từ tính.
- Đai mỏng riêng biệt các thông số của mô hình lý
thuyết được thống kê trong Bảng 1 (những giá trị ở trong ngoặc đơn).
Các mô hình của ranh giới tiếp xúc từ tính và đai
mỏng đều được tính toán với độ từ khuynh khu vực là 30o, độ từ thiên
là 0o và đều giả thiết chỉ có từ hoá cảm ứng đồng nhất.
Để tiện so sánh, ngoài những giá trị của các mô hình
lý thuyết, trong Bảng 1 còn giới thiệu các kết quả tính mô hình. Từ bảng này có
thể nhận thấy là phương pháp giải chập Euler mở rộng được thực hiện cho kết quả
rất tốt đối với ranh giới tiếp xúc và đai mỏng riêng biệt. Vị trí, độ sâu, góc
nghiêng, độ tương phản từ cảm của ranh giới tiếp xúc và đai mỏng xác định được
bằng phương pháp này gần như trùng với các thông số của mô hình (Bảng 1). Còn
đối với các nguồn gần nhau tạo ra hiệu ứng giao thoa - ví dụ như các ranh giới
tiếp xúc từ tính (Hình 2) và nhiều đai mỏng (Hình 3), thì phương pháp này cũng
cho kết quả khá tốt trong việc xác định vị trí, độ sâu, góc nghiêng và độ tương
phản từ cảm. Những tính toán của chúng tôi đều được thực hiện với cửa sổ trượt
là 10 điểm và ngưỡng tỷ lệ phần trăm để chọn nghiệm là 10% với sai số là độ
lệch chuẩn của các nghiệm tìm được. Như vậy các kết quả áp dụng phương pháp này
đối với những mô hình lý thuyết ở vùng vĩ độ thấp là khá tốt.
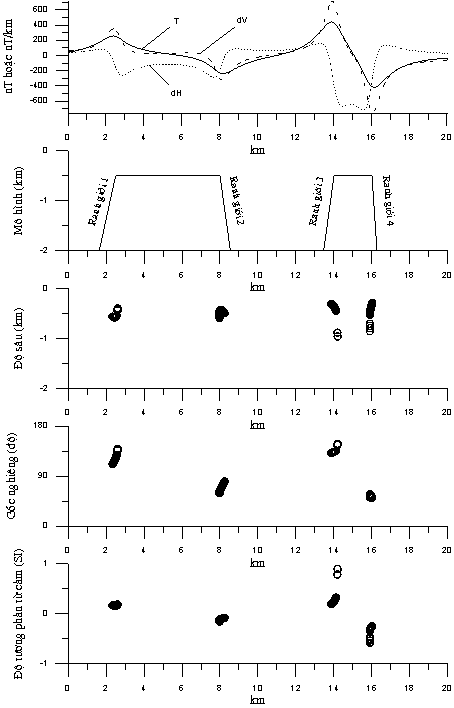
Hình 2. Mô
hình 4 ranh giới từ tính, giá trị trường dị thường (T), đạo hàm nằm ngang (dH),
đạo hàm thẳng đứng (dV) và kết quả xác định vị trí, độ sâu, góc nghiêng,
độ tương phản từ cảm của chúng
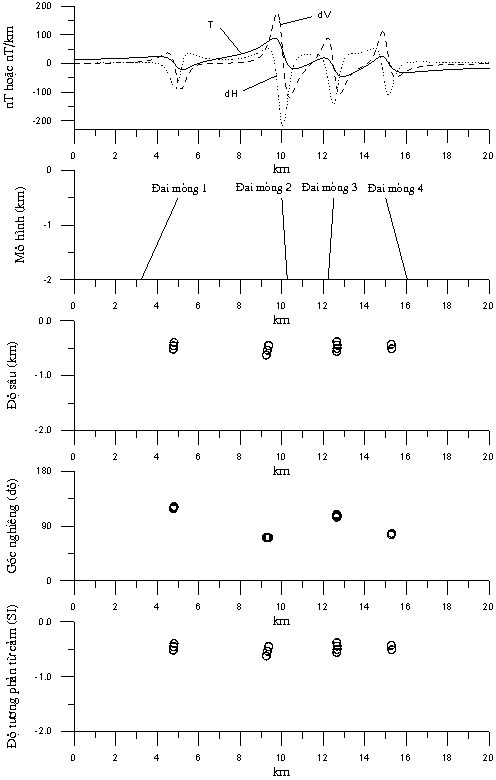
Hình 3. Mô hình 4 đai
mỏng, giá trị trường dị thường (T), đạo hàm nằm ngang (dH),
đạo hàm thẳng đứng (dV) và kết quả xác định vị trí, độ sâu, góc nghiêng,
độ tương phản từ cảm của chúng
Bảng
1. Kết quả tính toán đối với các mô hình
ranh giới và đai mỏng.
Giá trị trong ngoặc đơn là các thông số của mô hình
|
Mô hình
|
Độ sâu (m)
|
Góc nghiêng (độ)
|
Độ tương phản từ cảm (SI)
[x độ dày đối với đai]
|
|
Một ranh
giới
|
500 ± 0
(500)
|
110 ± 0 (110)
|
0,126 ±
0 (0,126)
|
|
Một đai mỏng
|
500 ± 3
(500)
|
110 ± 0
(110)
|
6,3 ±
0,015 (6,3)
|
|
Ranh
giới 1
|
536 ± 60
(500)
|
124 ± 8
(120)
|
0,083 ±
0,004 (0,063)
|
|
Ranh
giới 2
|
478 ± 47
(500)
|
66 ± 6
(70)
|
-0,058 ±
0,011 (0,063)
|
|
Ranh
giới 3
|
419 ±
181 (500)
|
135 ± 4
(110)
|
0,155 ±
0,095 (0,126)
|
|
Ranh
giới 4
|
469 ±
162 (500)
|
55 ± 2
(80)
|
-0,163 ±
0,05 (0,126)
|
|
Đai mỏng
1
|
452 ± 60
(500)
|
121 ± 2
(140)
|
7,212 ±
0,155 (12,6)
|
|
Đai mỏng
2
|
533 ± 86
(500)
|
71 ± 1
(80)
|
21,85 ± 0,386
(18,9)
|
|
Đai mỏng
3
|
468 ± 77
(500)
|
107 ± 2
(100)
|
9,944 ±
0,356 (12,6)
|
|
Đai mỏng
4
|
466 ± 58
(500)
|
77 ± 2
(55)
|
7,514 ±
0,222 (12,6)
|
Với mục đích khẳng định khả năng của phương
pháp giải chập Euler mở rộng, chúng tôi đã áp dụng phương pháp này để luận giải
tuyến số liệu dị thường từ hàng không Nam Định - Hải Phòng nằm ở phía đông nam
Hà Nội. Dưới đây,
chúng tôi xin trình bày các kết quả đã đạt được khi áp dụng phương pháp này.
IV. ÁP DỤNG VỚI SỐ LIỆU THỰC TẾ
Tuyến số liệu dùng để luận giải được lấy từ bản
đồ dị thường từ hàng không DTa và có hướng tây nam - đông bắc với tọa độ điểm đầu
tuyến là 20o09'00'' vĩ độ Bắc, 105o58'39" kinh độ
Đông và tọa độ điểm cuối tuyến là 20o47'20'' vĩ độ Bắc, 106o45'01''
kinh độ Đông. Tuyến này dài khoảng 107 km và nằm gần như trùng với tuyến đo từ
telur Nam
Định - Hải Phòng của Nguyễn Thị Kim Thoa và nnk [9].
Vùng mà tuyến đo cắt qua nằm ở phía tây bắc trũng
Sông Hồng thuộc miền võng Hà Nội và bị lớp trầm tích Kainozoi phủ [2]. Trầm
tích Kainozoi ở trũng Sông Hồng hình thành theo sáu chu kỳ kiến tạo từ Eocen
đến Đệ tứ, tức là nó bắt đầu hình thành từ 38-32 Tr.n trước [16]. Trên bản đồ
địa chất, biểu hiện của các đứt gãy kiến tạo chính trong vùng nghiên cứu chỉ là
giả định. Tuy nhiên, các kết quả nghiên cứu địa chất kiến tạo và địa vật lý đã
khẳng định trũng Sông Hồng bị khống chế bởi ba đứt gãy chính là Sông Hồng, Sông
Chảy và Sông Lô [3, 10, 16].
Chúng tôi đã áp dụng phương pháp giải chập Euler mở
rộng cho tuyến số liệu dị thường từ hàng không Nam Định - Hải Phòng với chỉ số
cấu trúc là 0, kích thước cửa sổ là 10 điểm và ngưỡng tỷ lệ phần trăm để chọn nghiệm
là 10% với mục đích xác định một số ranh giới từ tính và bề dày của lớp phủ
trầm tích từ mặt đất đến đỉnh của các ranh giới tương phản từ tính. Kết quả xác
định vị trí, độ sâu, góc nghiêng và độ tương phản từ cảm được trình bày ở Hình
4.
Nói chung, giá trị độ tương phản từ cảm trong
vùng nghiên cứu là nhỏ. Trên cơ sở các kết quả tính toán được, chúng tôi đã
tiến hành mô hình hoá các cấu trúc chính bằng phần mềm Mag2dc. Phương pháp giải
chập Euler mở rộng phụ thuộc vào các giá trị đạo hàm nằm ngang và đạo hàm thẳng
đứng của trường dị thường từ quan sát được, do vậy, đối với những vùng mà trường
có độ phân dị rõ nét của các dị thường từ thì kết quả tính toán được khá tốt;
tuy nhiên, đối với những vùng mà trường bình ổn thì kết quả tính toán sẽ gặp
sai số khá lớn. Chính vì lý do này, khi tiến hành mô hình hóa đoạn tuyến từ
khoảng 50 đến 90 km, chúng tôi đã tham khảo thêm các kết quả đo từ telur tuyến
Nam Định - Hải Phòng về độ sâu đến đỉnh của các ranh giới tương phản từ tính.
Kết quả mô hình hoá đạt được khá tốt khi so sánh giá trị trường đo được và giá
trị trường tính toán từ mô hình.
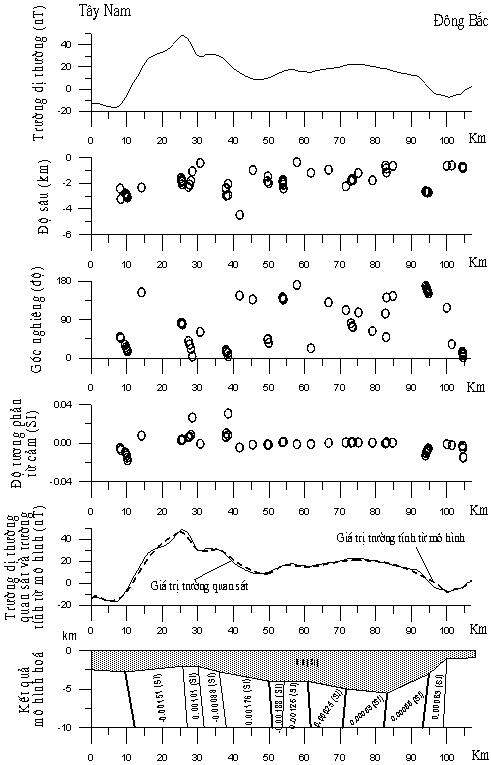
Hình 4. Kết
quả luận giải tuyến dị thường từ hàng không Nam Định - Hải Phòng
bằng phương pháp giải chập Euler mở rộng và mô hình hóa
Một số ranh giới từ tính xác định được có lẽ
tương ứng với một số đứt gãy chính trong vùng nghiên cứu (những ranh giới này
được vẽ đậm hơn ở phần kết quả mô hình hóa của Hình 4). Chẳng hạn như ranh giới
tương phản từ tính xác định được ở khoảng 10 km kể từ đầu tuyến với độ sâu đến
đỉnh khoảng 2,8 km và có góc nghiêng hướng về phía đông bắc, theo chúng tôi ứng
với đứt gãy Sông Hồng. Ranh giới tương phản từ tính ở khoảng gần 50 km có độ
sâu đến đỉnh khoảng 4 km, với góc nghiêng hướng về phía Đông Bắc có lẽ ứng với
đứt gãy Sông Chảy. Ranh giới tương phản từ tính ở khoảng hơn 60 km có độ sâu
đến đỉnh khoảng 4 km và có góc nghiêng hướng về phía đông bắc có lẽ ứng với đứt
gãy Thái Bình. Ở khoảng hơn 70 km dọc theo tuyến đo, ranh giới tương phản từ
tính có độ sâu đến đỉnh khoảng 5 km với góc nghiêng hướng về phía tây nam có lẽ
ứng với đứt gãy Vĩnh Ninh. Ranh giới tương phản từ tính ở khoảng hơn 80 km với
độ sâu đến đỉnh khoảng 5,5 km và góc nghiêng hướng về phía tây nam, theo chúng
tôi ứng với đứt gãy Sông Lô. Ranh giới tương phản từ tính ở khoảng 95 km có độ
sâu đến đỉnh khoảng 3 km và góc nghiêng hướng về phía Tây Nam, theo chúng tôi
ứng với đứt gãy Kiến Thụy. Những kết quả này khá phù hợp với một số nghiên cứu
trước đây cả về vị trí cũng như góc nghiêng của các đứt gãy này [3, 10, 16].
Nhìn chung, theo chúng tôi, bề dày của lớp phủ trầm tích Kainozoi trong vùng
nghiên cứu đến đỉnh của các ranh giới tương phản từ tính biến đổi trong khoảng
từ hơn 2 đến 5,5 km và phần sâu nhất nằm ở vùng giữa đứt gãy Vĩnh Ninh và đứt
gãy Sông Lô; tuy nhiên ở phần cuối tuyến, lớp phủ này mỏng hơn (khoảng 1 km).
KẾT LUẬN
Bước
đầu áp dụng phương pháp giải chập Euler mở rộng đối với mô hình lý thuyết và số
liệu thực tế đã cho phép chúng tôi khẳng định rằng phương pháp này có thể sử
dụng có hiệu quả trong việc luận giải tuyến số liệu dị thường từ trên lãnh thổ
Việt Nam.
Đối với những vùng mà trường dị thường từ bình ổn, không có sự phân dị rõ nét
của các dị thường từ, chúng ta cần phải kết hợp với một số phương pháp địa vật
lý khác trong quá trình luận giải. Phương pháp này cho phép xác định được vị
trí, độ sâu (thường là đến đỉnh của vật thể gây dị thường), góc nghiêng và độ
tương phản từ cảm. Đây là những thông tin hết sức hữu ích và cần thiết trong
việc luận giải địa chất các tài liệu dị thường từ, góp phần quan trọng vào việc
nghiên cứu địa chất nói chung và tìm kiếm, thăm dò khoáng sản nói riêng.
Lời cám ơn: Tác giả xin chân thành cảm
ơn GS. TSKH. Phạm Năng Vũ, TS. Lê Huy Minh đã có những ý kiến đóng góp quý báu
và xác đáng trong việc hoàn chỉnh bài báo này. Tác
giả cũng trân trọng cảm
ơn ThS. Lưu Việt Hùng đã
giúp đỡ trong quá trình mô hình hóa. Bài báo được hoàn thành với sự tài
trợ của Hội đồng Khoa học tự nhiên.
VĂN LIỆU
1. Barbosa V.C.F., Silva
J.B.C., Medeiros W.E., 1999. Stability analysis and
improvement of structural index estimation in Euler deconvolution. Geophysics, 64 : 48-60.
2. Cục Địa chất và Khoáng sản Việt Nam.
Các tờ bản đồ địa chất tỉ lệ 1: 200
000. Trung tâm Thông tin - Lưu trữ Địa chất phát hành. Hà Nội.
3. Đào Ngọc Tường, Phạm Năng Vũ, 2000. Cấu trúc sâu của đới
đứt gãy Sông Hồng theo kết quả xử lý tổng hợp các số liệu địa chấn và trọng
lực. TC Các khoa học về Trái đất, 22/4: 380-287. Hà Nội.
4. Fairhead J. D., Bennet K. J., Gorden D. R. H. and Huang
D., 1994.
Euler: Beyond the “Black Box”. 64th Ann. Internat. Mtg. Soc.
Expt. Geophys., Expanded Abstracts, 422-424.
5. Kuttikul P., 1995. Optimization of 3D Euler deconvolution for the
interpretation of potential field data. M.S.
thesis Intern. Training Centre, Delft.
6. Lưu Việt
Hùng, Lê Huy Minh, Võ
Thanh Sơn, 2005. Phương pháp giải
chập Werner nhiều nguồn trong luận giải tuyến số liệu dị thường từ. Tuyển
tập báo cáo HNKH-KT Địa vật lý Việt Nam lần 4, 71-83. Hà Nội.
7. Mushayandebvu M. F., Driel P. V., Reid A. B., Fairhead J.
D., 2001. Magnetic
source parameters of two-dimensional structures using extended Euler
deconvolution. Geophysics, 66: 814-823.
8. Nabigian M. N., 1972. The analytic
signal of two-dimensional magnetic bodies with polygonal cross section. Geophysics, 37: 507-517.
9. Nguyễn Thị Kim Thoa (Chủ
biên), 1996.
Khảo sát nước ngầm tại đồng bằng sông Cửu Long và đồng bằng Sông Hồng bằng tổ
hợp phương pháp từ tellua và đo sâu điện. Đề
án điều tra cơ bản cấp Nhà nước. Lưu trữ Viện Vật lý Địa cầu, Hà Nội.
10. Phạm Năng Vũ, 2000. Quá trình biến
dạng của đới đứt gãy Sông Hồng trong Kainozoi. TC Các khoa học về Trái đất,
22/4: 278-289. Hà Nội.
11. Press W. H., Flannery B. P., Teukolsky S. A., Vetterling
W. T., 1989. Numerical
recipes, the art of scientific computing. Cambridge University Press.
12. Reid A. B., Allsop J. M., Granser H.,
Millett A.J ., Somerton I. W., 1990. Magnetic interpretation in
three dimensions using Euler deconvolution. Geophysics,
55:
80-91.
13. Reid A. B., 1995. Euler deconvolution,
past, present and future: A review. 65th Ann. Intern. Mtg. Soc.
Expt. Geophys., Expanded Abstracts, 272-273.
14. Silva J. B. C., Barbosa V. C. F., Medeiros
W. E., 2001. Scattering, symmetry and bias analysis of source-position
estimates in Euler deconvolution and its practical implications. Geophysics, 66: 1149-1156.
15. Thompson D. T., 1982. A new technique
for making computer-assisted from magnetic data. Geophysics, 47: 31-37.
16. Trần Nghi, Chu
Văn Ngợi, Đinh Xuân Thành, Nguyễn Đình Nguyên, 2000. Tiến hoá trầm tích Kainozoi
bồn trũng Sông Hồng trong mối quan hệ với hoạt động kiến tạo. TC Các khoa
học về Trái đất, 22/4: 290-305. Hà
Nội.
![]() trong mặt phẳng 2-D; như vậy M
thoả mãn phương trình sau [15]:
trong mặt phẳng 2-D; như vậy M
thoả mãn phương trình sau [15]:![]() (1)
(1)![]() , chúng biến đổi thế
, chúng biến đổi thế ![]() , thì từ sự bất biến này ta có:
, thì từ sự bất biến này ta có:![]() (2)
(2)![]() (3)
(3)![]() như vậy građien của trường sẽ là:
như vậy građien của trường sẽ là:![]() (4)
(4)![]() (5)
(5)![]() (6)
(6)![]() (7)
(7)![]() , với K là giá trị độ tương phản từ
cảm của ranh giới tiếp xúc, d là góc nghiêng, F là giá trị trường
toàn phần của Trái đất,
, với K là giá trị độ tương phản từ
cảm của ranh giới tiếp xúc, d là góc nghiêng, F là giá trị trường
toàn phần của Trái đất, ![]() , trong đó i là độ từ khuynh của
môi trường và A là góc giữa phương bắc từ và trục x, và tan(I)
= tan(i)/ cos(A). Thay thế vào các phương trình (1) và (2) ta có:
, trong đó i là độ từ khuynh của
môi trường và A là góc giữa phương bắc từ và trục x, và tan(I)
= tan(i)/ cos(A). Thay thế vào các phương trình (1) và (2) ta có:![]() (8)
(8)![]() (9)
(9)![]() (10)
(10)


