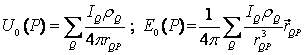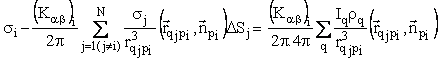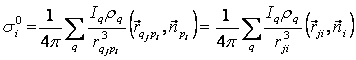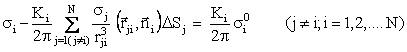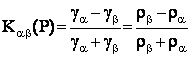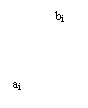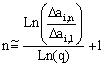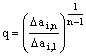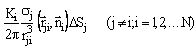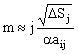NGHIÊN CỨU NÂNG CAO HIỆU QUẢ THUẬT TOÁN TÍNH MẬT ĐỘ ĐIỆN TÍCH THỨ CẤP TRÊN RANH GIỚI BẤT ĐỒNG NHẤT

VŨ ĐỨC MINH

Trường đại học Khoa học Tự nhiên, ĐHQGHN, Nguyễn Trãi, Thanh Xuân, Hà Nội

Tóm tắt: Bài báo giới thiệu thuật toán tính mật độ điện tích thứ cấp trên mặt ranh giới của môi trường đồng nhất từng phần trên cơ sở lý thuyết của phương pháp điện tích thứ cấp. Từ việc phân tích sự phụ thuộc của mật độ điện tích vào các yếu tố môi trường, tác giả đã giới thiệu các kết quả nghiên cứu và đề xuất thuật toán rời rạc hoá bề mặt ranh giới bất đồng nhất - quá trình tối ưu hoá việc phân chia và chọn lựa mạng lưới các phần tử yếu tố. Đồng thời, các kết quả áp dụng thuật toán này trên các môi trường bất đồng nhất từng phần, đặc biệt là kết quả từ một vài phương án khác nhau khi lựa chọn mạng lưới đối với cùng một môi trường để so sánh cũng được giới thiệu trong bài báo này. Các kết quả đã chứng minh cho sự cần thiết của việc nghiên cứu này, ngoài ra góp phần nâng cao tính chính xác, ưu điểm và hiệu quả của thuật toán nêu trên.

I. ĐẶT VẤN ĐỀ

Như chúng ta đã biết, có rất nhiều công trình công bố các phương pháp nghiên cứu mô hình nhằm giải bài toán thăm dò điện đối với môi trường phức tạp hai và ba chiều. Các công trình này chủ yếu tập trung theo hai hướng chính là phương pháp phương trình tích phân và phương pháp phương trình vi phân, trong đó công trình của Alpin [1] đã đưa ra công thức tổng quát tính mật độ điện tích thứ cấp cho môi trường bất đồng nhất có dạng là phương trình tích phân Fredolm loại 2, từ đó có thể tính thế, cường độ điện trường và điện trở suất của môi trường.

Tuy nhiên, các phương pháp này còn một nhược điểm là phải giải hệ phương trình đại số tuyến tính có số phương trình rất lớn, mặt khác thuật toán rời rạc hoá các yếu tố trên mặt các ranh giới bất đồng nhất như thế nào để đạt được các yêu cầu về tốc độ tính, độ chính xác vẫn còn là một vấn đề được nhiều người quan tâm hoàn thiện.

Trong bài báo này, chúng tôi xin giới thiệu một số kết quả bước đầu nghiên cứu quá trình rời rạc hoá các yếu tố trên mặt các ranh giới bất đồng nhất nhằm nâng cao hiệu quả thuật toán tính mật độ điện tích thứ cấp khi áp dụng phương pháp điện tích thứ cấp nhằm góp phần giải quyết mục tiêu trên.

II. THUẬT TOÁN TÍNH MẬT ĐỘ ĐIỆN TÍCH THỨ CẤP

Trong các bài báo trước, chúng tôi đã giới thiệu phương pháp điện tích thứ cấp và thuật toán tính mật độ điện tích thứ cấp trên mặt ranh giới của môi trường đồng nhất từng phần. Có thể tóm tắt như sau:

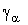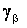Trong trường hợp môi trường đồng nhất từng phần, được phân chia bởi các mặt ranh giới S_ab mà g = 1/r có giá trị và có dạng bất kỳ. Điện trường tại mỗi điểm là tổng của các trường sơ cấp và thứ cấp.

Thế và trường sơ cấp tại điểm quan sát P được sinh bởi nguồn điểm hay hệ nguồn điểm của hệ cực phát được tính theo công thức:

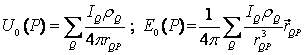(2.1)

ở đây r_QP - khoảng cách từ điện cực phát A_Q tới điểm P; r_Q là điện trở suất thật tại lân cận điểm Q; 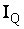- dòng do điện cực phát gây ra tại P.

Mặt ranh giới bất đồng nhất S_ab có dạng bất kỳ, không biểu diễn được bằng biểu thức giải tích nên bằng phương pháp số phải chia các mặt biên này thành N phần tử (yếu tố) DS_i sao cho trên đó có thể xem hàm dưới dấu tích phân là không đổi. Mỗi phần tử mặt DS_i có vị trí xác định bởi tọa độ của tâm phần tử, biểu diễn theo ba thành phần (x_i, y_i, z_i) và có hướng xác định bởi vectơ pháp tuyến đơn vị .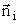

Tích phân theo mặt S_ab được rời rạc hóa dẫn đến hệ phương trình đại số tuyến tính với ẩn là mật độ điện tích thứ cấp s_i :

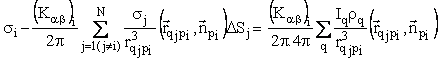(2.2)

(j ¹ i ; i = 1,2, ... N)

Nếu đặt: 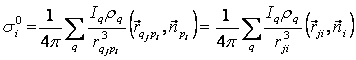(2.3)

là mật độ điện tích thứ cấp do trường sơ cấp tạo nên thì ta có thể đưa (2.2) về dạng:

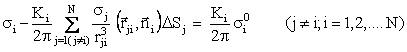(2.4)

với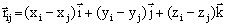

trong đó: 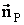- pháp tuyến tại điểm P của mặt phân chia S_ab

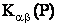- giá trị hệ số của bề mặt tiếp xúc (hệ số tương phản độ dẫn điện) tại P:

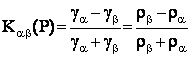(2.5)

Từ đó ta xác định được giá trị điện trở suất biểu kiến:

(2.6)

với: K(r) - hệ số hệ cực đo; I - cường độ dòng phát; DU - hiệu điện thế giữa cặp cực thu.

III. THUẬT TOÁN RỜI RẠC HOÁ CÁC RANH GIỚI BẤT ĐỒNG NHẤT

Sự gần đúng trong phép rời rạc tích phân mặt càng cao khi chia càng nhỏ các phần tử diện tích. Tuy nhiên điều này sẽ dẫn đến hệ rất nhiều phương trình, làm tăng rất lớn khối lượng tính toán để giải hệ phương trình (2.2). Vấn đề là phải chia kích thước các phần tử như thế nào để cho kết quả có mức độ gần đúng chấp nhận được mà khối lượng tính toán nhỏ nhất.

Từ phương trình (2.4), có thể nhận thấy rằng, độ lớn mật độ điện tích thứ cấp s_i tại phần tử i phụ thuộc hệ số tương phản độ dẫn điện K_i và mật độ điện tích thứ cấp do trường sơ cấp gây ra 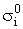. Do mật độ này giảm tỉ lệ nghịch theo khoảng cách r tính từ nguồn, có thể chia mặt ranh giới thành các phần tử có diện tích không đều: kích thước phần tử tăng theo khoảng cách đến nguồn và giảm theo độ lớn của hệ số tương phản độ dẫn điện. Cách chia mặt biên thành những phần tử không đều một cách thích hợp sẽ làm giảm số phương trình và rút ngắn thời gian thực hiện tính toán mà không ảnh hưởng đến độ chính xác của kết quả. Ngoài sự phụ thuộc vào các đại lượng nêu trên, mật độ điện tích thứ cấp tại mỗi phần tử chịu tác dụng bởi trường gây ra do các điện tích thứ cấp khác. Do đó, ứng với mỗi phần tử, khi tính toán trường gây bởi những nguồn thứ cấp lân cận, cần chia nhỏ các phần tử gây ảnh hưởng này để giảm sai số do kích thước phần tử trở nên đáng kể đối với khoảng cách tính trường. Vấn đề đặt ra là cần phải nghiên cứu tối ưu hoá việc rời rạc hoá các phần tử của mặt ranh giới bất đồng nhất.

Mô hình nửa không gian được phân chia thành những miền đồng nhất từng phần bởi những mặt biên S_ab. Các mặt biên được rời rạc hóa thành các phần tử mặt có kích thước đủ nhỏ so với khoảng cách đến nguồn. Các phần tử có thể có dạng bất kỳ là tam giác, tứ giác hay đa giác.... để mô phỏng chính xác dạng mặt biên. Việc phân chia này được tùy chọn sao cho thỏa mãn điều kiện đủ nhỏ của các phần tử đối với khoảng cách tính trường. Trong nghiên cứu mô hình, chúng tôi có thể giải quyết vấn đề rời rạc hóa mặt bất kỳ nhờ công cụ đồ họa trên màn hình máy tính. Tuy nhiên để tạo thuận tiện cho việc xây dựng mô hình, tính toán trong phạm vi gần đúng cho phép, có thể chọn các phần tử này là những mặt chữ nhật đủ nhỏ.

Có thể xem mặt biên S_ab gồm các mặt chữ nhật xác định bởi các cặp cạnh (a_i, b_i). Mỗi mặt chữ nhật này được chia thành các phần tử mặt có kích thước không đều cạnh D_aij, D_bij (Hình 1). Độ lớn các cạnh phần tử được chọn theo tỉ lệ đối với hệ số tương phản độ dẫn điện và khoảng cách tính từ nguồn. Đối với bất đồng nhất kéo dài vô hạn hay cắm sâu vào môi trường, có thể giới hạn khoảng cách đủ xa đối với nguồn và chia kích thước lớn dần theo chiều kéo dài. Tiến trình rời rạc hóa mặt biên bất đồng nhất thành các phần tử mặt như sau:

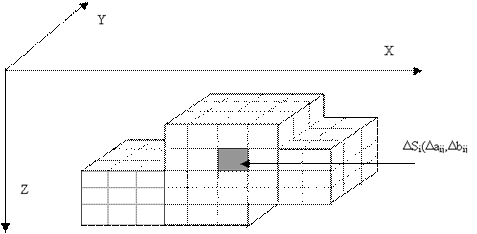
Hình 1. Rời rạc mặt biên bất đồng nhất thành những mặt chữ nhật

Xét từng cạnh a_i (hay b_i), so sánh độ lớn cạnh này với độ lớn của đại lượng:

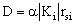(3.1)

trong đó: a - hệ số phân chia được chọn trong khoảng (0,1), K_i - hệ số tương phản độ dẫn điện tại cạnh a_i, r_si - khoảng cách từ tâm của cạnh a_i đến nguồn phát.

Nếu độ lớn a_i £ D thì cạnh này được chọn tương ứng cạnh một phần tử.

Ngược lại, thực hiện sự phân chia độ lớn cạnh này thành n đoạn đủ nhỏ Da_ij có kích thước tăng theo cấp số nhân như sau:

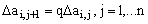(3.2)

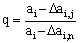với: (3.3)

Vì số phần tử n dọc theo mỗi cạnh là số nguyên và thỏa mãn: 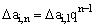, nên n được tính bởi:

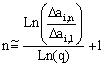(3.4)

Công bội q và độ lớn của cạnh phần tử được tính lại thích hợp:

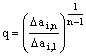(3.5)

(3.6)

Tiến trình thực hiện cho tất cả các mặt con của mặt biên bất đồng nhất. Thuật toán rời rạc hóa mặt biên bất đồng nhất thành những phần tử có kích thước không đều làm giảm số phương trình đại số tuyến tính (2.2) nhờ đó lời giải của bài toán thu được độ chính xác chấp nhận được với thời gian rút ngắn đáng kể.

Do cơ chế gây trường thứ cấp giữa các phần tử, cần nâng cao tính gần đúng khi tính trường sinh bởi các phần tử lân cận, khi đó khoảng cách trở nên có độ lớn đáng kể so với kích thước phần tử (Hình 2).

Hình 2. Rời rạc hóa phần tử mặt

Từ phương trình (2.4) ta thấy số hạng thứ hai của vế trái là tổng các số hạng:

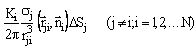(3.7)

Trong (3.7), biểu thức tích vô hướng chứa tham số khoảng cách a_ij giữa phần tử thứ j và điểm tính trường i, vì vậy thuật giải công đoạn này được thực hiện như sau:

So sánh a_ik với kích thước phần tử j, nếu:

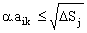(3.8)

thì rời rạc hóa cạnh phần tử j thành m đoạn, với m là số nguyên được làm tròn bởi biểu thức:

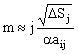với a < 1, số nguyên j > 1 (3.9)

Với quá trình rời rạc hóa các mặt biên thành các phần tử mặt có kích thước không đều và hợp lý, đồng thời tính đến cả ảnh hưởng của các phần tử yếu tố xung quanh nên thuật toán tính mật độ điện tích thứ cấp được nhanh chóng và chính xác hơn.

IV. THÍ DỤ ÁP DỤNG

1. Chúng tôi đã lập chương trình bằng ngôn ngữ MATLAB [2] chạy trên máy vi tính để thử nghiệm thuật toán tính mật độ điện tích thứ cấp với các quá trình rời rạc hoá khác nhau như đã trình bày ở trên đối với một số mô hình môi trường đồng nhất từng phần để so sánh. Dưới đây là một kết quả ví dụ minh hoạ.

Mô hình thử nghiệm là nửa không gian có một mặt phân chia môi trường thành 2 lớp có điện trở suất tương ứng là r₁, r₂ (Hình 3). Mặt phân chia gồm 3 phần:

- Phần thứ nhất nằm song song với mặt môi trường có độ sâu h₁, gọi là mặt h₁.

- Phần thứ hai nằm nghiêng với mặt môi trường một góc a gọi là mặt nghiêng.

- Phần thứ ba cũng nằm song song với mặt môi trường có độ sâu h₂, gọi là mặt h₂.

Sử dụng hệ tọa độ Descartes các với gốc tọa độ O đặt ở hình chiếu giao điểm giữa hai mặt h₁ và mặt nghiêng lên mặt môi trường, trục z hướng xuống dưới.

O

Hình 3. Mô hình thử nghiệm

Chiều dài của lưới chia lớn hơn 100 lần độ sâu h₁, tại gần cực phát và mặt nghiêng lưới chia sao cho các yếu tố phần tử mặt có diện tích như nhau, còn càng xa cực phát thì diện tích các yếu tố phần tử mặt càng lớn dần với công bội theo thang logarit là 1,2. Số yếu tố phần tử mặt có diện tích đều là 70, số yếu tố phần tử mặt có diện tích không đều là 60.

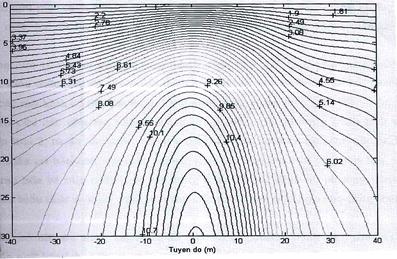
Kết quả mặt cắt đẳng trị điện trở suất biểu kiến ứng với mô hình bậc nghiêng góc 30⁰ có các tham số r₁ = 10 Wm, h₁ = 10 m, h₂ = 20 m, r₂ = 0.1 Wm trong trường hợp này được biểu diễn trên Hình 4, cực phát đặt tại điểm O và lấy làm gốc toạ độ.

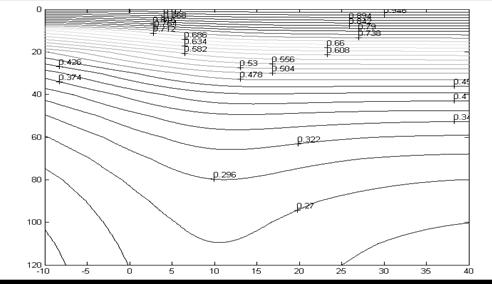
Hình 4. Mặt cắt đẳng trị điện trở suất biểu kiến ứng với mô hình biểu diễn ở Hình 3
(phương án 1)

Cũng với mô hình thử nghiệm nêu trên, chúng tôi tính toán với một lưới chia tương tự nhưng có bước chia sít hơn, tức là số yếu tố phần tử trên lưới là như nhau nhưng tổng toàn bộ chiều dài lưới chỉ cỡ 50 lần độ sâu h₁ thì kết quả phản ánh không phù hợp với mô hình nghiên cứu (Hình 5), chứng tỏ các điện tích thứ cấp ở ngoài lưới chia vẫn còn ảnh hưởng đáng kể đến trường điện thứ cấp của mặt ranh giới gây ra tại điểm quan sát.

Kết quả mặt cắt đẳng trị điện trở suất biểu kiến ứng với mô hình bậc nghiêng góc 30⁰ có các tham số r₁ = 10 Wm, h₁ = 10 m, h₂ = 20 m, r₂ = 0.1 Wm trong trường hợp này được biểu diễn trên Hình 5, cực phát đặt tại điểm O và lấy làm gốc toạ độ.

Nếu ta chia mạng lưói như trong trường hợp này nhưng có chiều dài toàn bộ lưới cỡ 100 lần độ sâu h₁, có nghĩa là số yếu tố diện tích mặt tăng lên gần gấp đôi thì thời gian tính toán sẽ tăng lên gấp hơn 3 lần mặc dù kết quả không thay đổi nhiều so với kết quả biểu diễn trên Hình 4. Điều này càng khẳng định đến vai trò quyết định của thuật toán rời rạc hoá các mặt ranh giới bất đồng nhất như đã trình bày ở trên.

2.Từ mô hình như biểu diễn trên Hình 3, khi thay đổi các thông số của môi trường ta sẽ có một số mô hình khác hay gặp trong thực tế. Đây là một ưu điểm của việc chọn mô hình thử nghiệm. Chúng tôi cũng đã lập chương trình bằng ngôn ngữ MATLAB để tính mật độ điện tích thứ cấp với thuật toán rời rạc hoá đã được nêu trên đối với một số mô hình môi trường đồng nhất từng phần biến tấu của Hình 3. Dưới đây là một số kết quả ví dụ minh hoạ.

Kết quả mặt cắt đẳng trị điện trở suất biểu kiến ứng với mô hình có một bậc dạng xung vuông góc (Hình 6) với các tham số r₁ = 1 Wm, h₁ = 10 m, h₂ = 16 m, r₂ = 10 Wm được biểu diễn trên Hình 6, cực phát đặt tại điểm O (hình chiếu của mặt biên thẳng đứng bên trái lên mặt môi trường) và lấy làm gốc toạ độ.

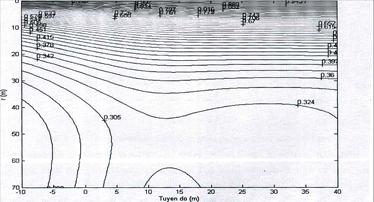
Hình 5. Mặt cắt đẳng trị điện trở suất biểu kiến ứng với mô hình biểu diễn ở Hình 3
(phương án 2)

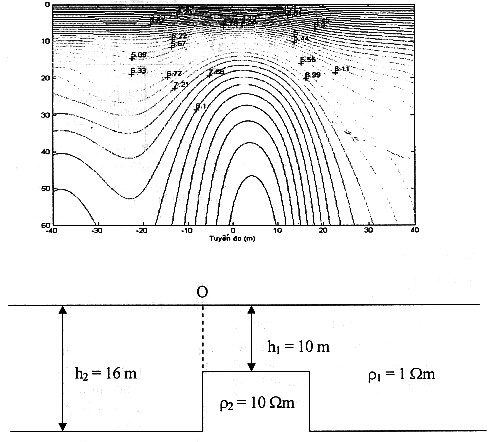
Hình 6. Mặt cắt đẳng trị điện trở suất biểu kiến ứng với mô hình có một bậc dạng xung vuông góc

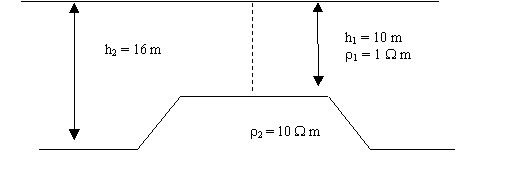
Kết quả mặt cắt đẳng trị điện trở suất biểu kiến ứng với mô hình có một bậc dạng hình thang (Hình 7) với các tham số r₁ = 1 Wm, h₁ = 10 m, h₂ = 16 m, r₂ = 10 Wm được biểu diễn trên Hình 7, cực phát đặt tại điểm O (hình chiếu điểm giữa mặt nằm ngang ở chiều sâu h₁ của bậc dạng hình thang lên mặt môi trường) và lấy làm gốc toạ độ.

O

Hình 7. Mặt cắt đẳng trị điện trở suất biểu kiến ứng với mô hình có bậc dạng hình thang

V. KẾT LUẬN

Nghiên cứu nâng cao hiệu quả thuật toán chọn lựa mạng lưới rời rạc hóa bề mặt ranh giới bất đồng nhất để tính mật độ điện tích thứ cấp trên các ranh giới bất đồng nhất là một việc làm hết sức cần thiết, có ý nghĩa cả về khoa học và kinh tế.

Qua bước đầu nghiên cứu thử nghiệm, chúng tôi thấy có một số vấn đề cần lưu ý sau:

1) Mạng lưới phải được chọn đủ xa nguồn phát để có thể đảm bảo mô phỏng toàn bộ cấu trúc bất đồng nhất của môi trường, đồng thời sự sai khác do ảnh hưởng của các điều kiện biên gây ra không đáng kể.

2) Để giảm thiểu số phương trình cần thiết khi tính toán nhưng vẫn đảm bảo độ chính xác chấp nhận được, ta phải rời rạc hoá theo kích thước không đều của các phần tử. Các phần tử càng gần nguồn có kích thước càng nhỏ, đồng thời các phần tử gần điểm đo cũng cần phải có kích thước đủ nhỏ vì chúng ảnh hưởng lớn đến kết quả tính toán.

3) Tại những nơi mà môi trường và các bất đồng nhất có độ tương phản về tính chất điện càng lớn thì càng phải chia nhỏ phần tử tại những nơi đó.

Như vậy, vấn đề trọng tâm của thuật toán này là phải chú ý đến độ hội tụ của lời giải, độ chính xác của kết quả và thời gian tính toán cần thiết. Chúng tôi cũng đã chú ý đến tính mềm dẻo, tiện ích của chương trình như khả năng thay đổi các thông số theo yêu cầu tính toán: khoảng cách giữa các phần tử yếu tố, số gia kích thước theo khoảng cách từ nguồn ..v.v. Chắc rằng thuật toán này còn cần phải tiếp tục nghiên cứu để nâng cao hiệu quả của phương pháp hơn nữa.

VĂN LIỆU

1. Alpin L.M., 1981. Metod vtoritchnykh zariadov. Prikladnaya geofizika, 99. Moskva.

2 Etter D.M. 1999. Engineering problem solving with Matlab. Prentice International Inc., University of Colorado Boulder, 423 p.