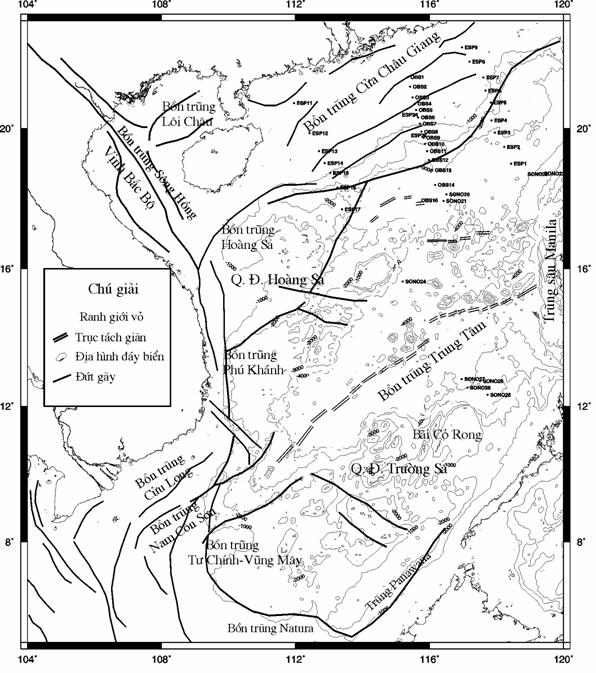
Hình 1. Bản đồ vị trí vùng nghiên cứu và hệ thống đứt
gãy chính trong vùng. Sono, ESP
và OBS kí hiệu vị trí các điểm đo sâu mặt Moho theo địa chấn [7, 11, 19, 23]. Thiết diện đường đồng mức địa hình đáy biển 1000 m
CẤU TRÚC MẶT MOHO KHU VỰC BIỂN ĐÔNG
NGUYỄN NHƯ TRUNG, NGUYỄN THỊ THU
HƯƠNG
Phân viện
Hải dương học tại Hà Nội, Hoàng Quốc Việt, Cầu Giấy, Hà Nội
Tóm tắt: Trong bài báo này, tài liệu trọng lực vệ tinh và địa
chấn sâu đã được sử
dụng để nghiên cứu độ sâu mặt Moho khu vực biển Đông trên cơ sở ba mô hình tính toán: mô hình đẳng tĩnh địa
phương, tương quan - hồi quy và bài toán ngược trực tiếp 3D. Kết quả so sánh với
các tài liệu địa chấn sâu cho thấy độ sâu mặt Moho tính được theo phương pháp
giải bài toán ngược 3D cho kết quả tốt nhất. Bản đồ mặt Moho xây dựng bằng bài
toán ngược 3D không chỉ cho độ sâu tuyệt đối mà còn có mối tương quan tốt nhất
với các cấu trúc địa chất và yếu tố kiến tạo trong khu vực. Các uốn lượn của mặt
Moho liên quan đến sự thành tạo và tiến hóa của biển Đông trong Kainozoi. So
sánh mặt Moho 3D với mặt Moho đẳng tĩnh và dị thường trọng lực có thể chia tình
trạng bù đẳng tĩnh trong khu vực làm: 1) trạng thái cân bằng đẳng tĩnh toàn phần
ở phía bắc, tây và tây nam của rìa lục địa; 2) trạng thái bù đẳng tĩnh đạt
80-90% ở bồn Trung tâm biển Đông và rìa nam; 3) đới hút chìm Manila có lẽ
là một đới đang hoạt động, trạng thái cân bằng đẳng tĩnh chưa được thiết lập.
MỞ ĐẦU
Bản đồ độ sâu mặt Moho khu vực Biển Đông đã được một số tác giả thành lập
trên cơ sở các số liệu đo trọng lực thành tàu hiện có [4]. Một trong những nhược
điểm lớn nhất của các bản đồ này là thành lập dựa trên các nguồn số liệu không
đồng nhất, độ đo phủ không đồng đều, đồng thời mô hình tính toán cũng thô sơ dẫn
đến mặt Moho bị làm trơn đi nhiều. Hơn nữa, độ sâu mặt Moho tính được có sự sai
khác lớn so với số liệu địa chấn sâu [10]. Các bản đồ này chỉ có thể cung cấp
cho chúng ta một bức tranh khái quát chung về mặt Moho khu vực biển Đông, khó có
thể thiết lập được mối tương quan chi tiết và tin cậy giữa các yếu tố cấu trúc -
kiến tạo trong khu vực với sự biến đổi của địa hình mặt Moho ở phía dưới [4].
Trên cơ sở nguồn số liệu trọng lực vệ tinh toàn cầu, có độ đồng nhất cao (2x2
phút), và 42 điểm độ sâu mặt Moho xác định theo địa chấn ở khu vực rìa bắc và
trũng Trung tâm biển Đông, N.N. Trung [9] đã xây
dựng phương trình hồi quy giữa mặt Moho và dị thường trọng lực manti Bouguer.
Bản đồ độ sâu mặt Moho này có độ chi tiết và chính xác cao so với các số liệu
địa chấn sâu hiện có tại rìa bắc và bồn trũng Trung tâm. Nó có thể cho phép
thiết lập mối tương quan giữa các yếu tố cấu trúc - kiến tạo trong khu vực với
sự biến đổi của địa hình mặt Moho phía dưới. Tuy nhiên, phương trình hồi quy này
được xây dựng trên cơ sở mối tương quan giữa mặt Moho và dị thường manti Bouguer
ở phần rìa bắc và bồn trũng Trung tâm, phần còn lại được coi như có cùng quy
luật. Thực tế có như vậy không vẫn còn là câu hỏi để ngỏ cần được kiểm nghiệm.
Trong bài báo này các tác giả trình bày phương pháp tính độ sâu mặt Moho có
tính ưu việt hơn so với các phương pháp đã được sử dụng trước đây, đó là phương
pháp giải bài toán ngược trực tiếp ba chiều (3D).
Phương pháp này dựa trên thuật toán của Parker [12], cho phép tính trực tiếp độ
sâu mặt Moho từ dị thường trọng lực qua miền tần số. Lời giải của bài toán ngược
3D được khống chế bởi số liệu địa chấn sâu có thể cho độ tin cậy cao. Các kết
quả tính toán cho phép khảo sát trạng thái cân bằng đẳng tĩnh của vỏ, mối tương
quan giữa địa hình mặt Moho, dị thường trọng lực và các yếu tố cấu trúc - kiến
tạo trong vùng.

Hình 1. Bản đồ vị trí vùng nghiên cứu và hệ thống đứt
gãy chính trong vùng. Sono, ESP
và OBS kí hiệu vị trí các điểm đo sâu mặt Moho theo địa chấn [7, 11, 19, 23]. Thiết diện đường đồng mức địa hình đáy biển 1000 m
I. KHÁI QUÁT VỀ CẤU TRÚC ĐỊA CHẤT BIỂN ĐÔNG
Biển Đông được hình
thành như là kết quả của quá trình căng giãn và gãy ra của lục địa Nam Trung Hoa
trong khoảng 32-15.5 triệu năm [3, 19, 20] theo phương gần B-N và
chuyển dần sang TB-ĐN (Hình 1). Kết quả của quá trình tách giãn đã hình thành
nên bồn trũng Trung tâm và các bồn trũng Đệ tam trên các rìa lục địa. Rìa bắc và
tây bắc có các bồn trũng Châu Giang, Nam Hải Nam (Hoàng Sa), bồn trũng Tây Nam
Đài Loan và bồn trũng Lôi Châu. Rìa nam có các bồn và phụ bồn Reed Bank,
Palawan, Châu Viên, Tiên Nữ, Tư Chính – Vũng Mây. Rìa tây và tây nam có các bồn
trũng Sông Hồng, Phú Khánh, Cửu Long, Nam Côn Sơn và Natuna. Địa tầng khu vực
được chia thành ba tầng chính [22, 23]: tầng cấu trúc dưới có tuổi Mesozoi – Paleozoi, tầng cấu
trúc giữa có tuổi Paleocen – Eocen và tầng cấu trúc trên có tuổi từ Oligocen
muộn đến hiện đại. Hai bất chỉnh hợp địa tầng khu vực phân chia ba tầng này thể
hiện hai pha kiến tạo lớn trong khu vực là kéo tách tạo rift (pull-apart/rift)
của lục địa Nam Trung Quốc và tách giãn đáy biển ở biển Đông [22, 23]. Về cấu trúc, xuất hiện các đứt gãy đơn nghiêng khống chế
các cấu trúc rìa bắc và nam bồn trũng Trung tâm [5,
6, 14].
Các đứt gãy này chủ yếu kéo dài theo phương ĐB-TN và Đ-T. Tại rìa tây, các cấu
trúc được đặc trưng bởi các đứt gãy dịch chuyển có phương chủ yếu là B-N, TB-ĐN
và ĐB-TN [9, 10, 15].
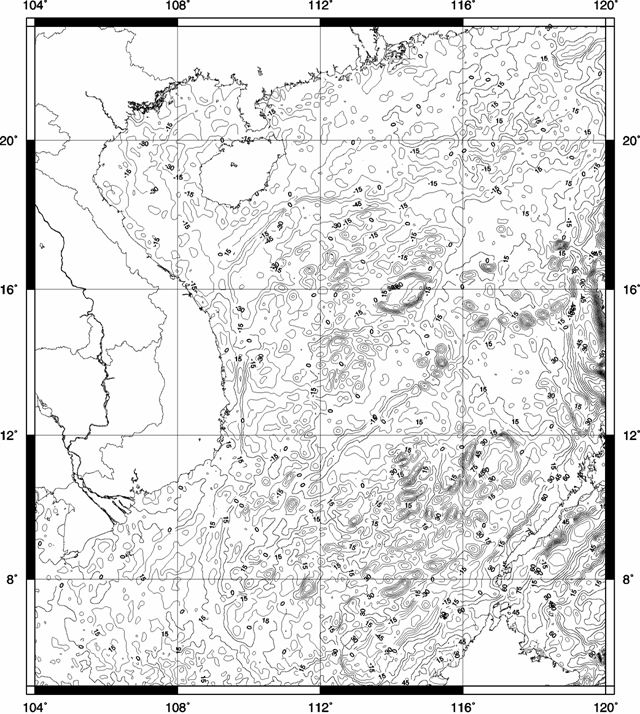
Hình 2a. Dị thường trọng lực vệ tinh Fai. Thiết diện
đường đồng mức 15 mGal
II. NGUỒN SỐ LIỆU SỬ DỤNG
Trong bài viết này
chúng tôi sử dụng nguồn số liệu dị thường trọng lực vệ tinh Fai và địa hình đáy
biển từ cơ sở dữ liệu toàn cầu của Viện Nghiên cứu Hải dương học Scripps, phiên
bản 9.2 [17] (xem hình 2a). Độ phân giải của nguồn số liệu là 2’x2’, sai
số bình phương trung bình của nguồn số liệu này với số liệu đo trọng lực thành
tàu khoảng 3.1-7 mGal [17]. Trên khu vực biển
Đông, kết quả so sánh trong trường hợp các điểm đo của tàu Gagarinski trùng với
lưới số liệu trên thì độ lệch bình phương trung bình là 4.0 mGal. Bề dày trầm
tích Kainozoi được thu thập và số hoá từ một số nguồn số liệu hiện có, sau đó
cộng với độ sâu địa hình đáy biển ta có độ sâu móng trước Kainozoi. 42 điểm độ
sâu mặt Moho từ các số liệu đo địa chấn sâu tại khu vực thềm lục địa và sườn lục
địa nam Trung Quốc và trũng sâu Biển Đông được thu thập từ các công trình của [7, 11, 19, 21].
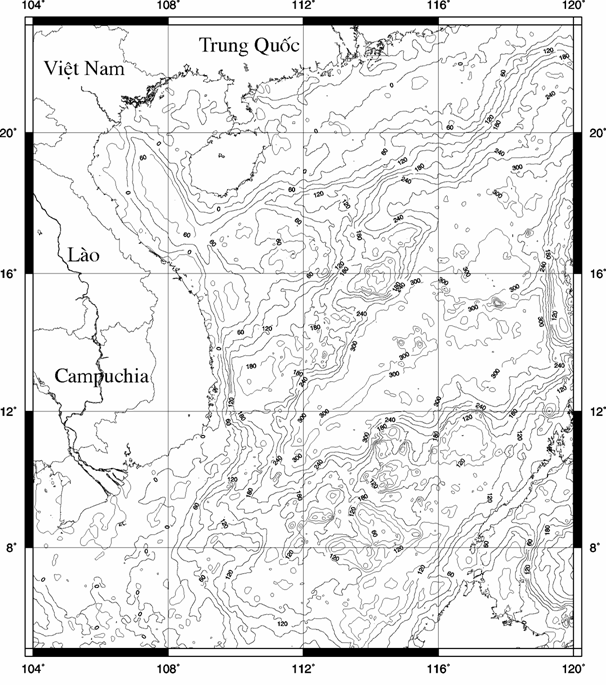
Hình 2b. Dị thường trọng lực dư do mặt Moho gây ra
được hiệu chỉnh từ dị thường Fai.
Thiết diện đường đồng mức 30 mGal
III. PHƯƠNG PHÁP XÁC ĐỊNH MẶT MOHO
1. Phương pháp bài toán ngược 3D
Mối quan hệ giữa địa hình
mặt ranh giới mật độ và dị thường trọng lực được biểu diễn tốt nhất thông qua
phép biến đổi Fourier hai chiều. Công thức biểu diễn mối quan hệ này như sau
[12]:
![]() (1)
(1)
trong đó: F[ ]
là toán tử biến đổi Fourier hai chiều; Dg - dị thường trọng lực; G- là hằng số hấp dẫn; Dr - là độ tương phản mật độ qua ranh
giới; k- số sóng; d - chiều sâu trung bình của ranh
giới; h (x,y)- độ cao của mặt ranh giới so với chiều sâu trung bình.
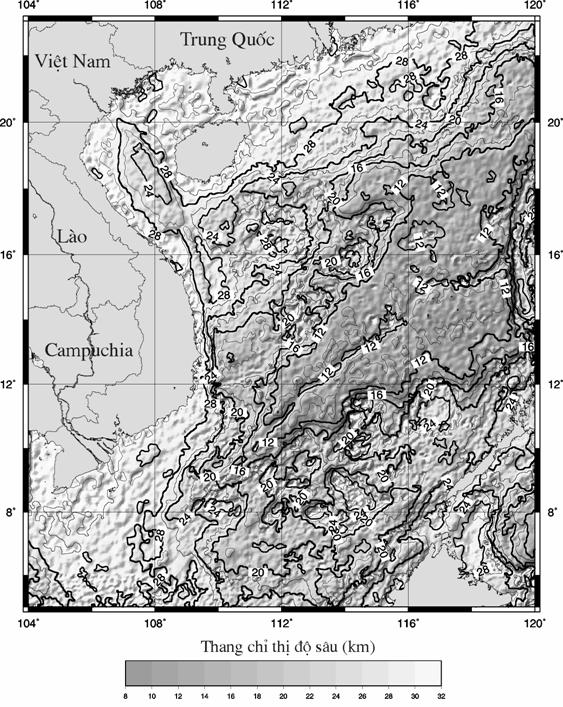
Hình 3. Bản đồ độ sâu mặt Moho
tính theo phương pháp bài toán ngược 3D.
Sai số so với số liệu đo địa chấn 5.6%.
Thiết diện đường đồng mức 2 km
Vế phải của công thức (1)
chỉ ra rằng khi địa hình mặt ranh giới nằm dưới mặt quan sát, gốc toạ độ được
chọn ở điểm trung bình của đường địa hình, thì chuỗi vô hạn trên hội tụ rất
nhanh (n = 4-5) [13]; khi biên độ cực đại của địa hình nhỏ hơn nhiều so với độ
sâu trung bình (d), thì giá trị của biểu thức (1) chủ yếu phụ thuộc vào số hạng
đầu tiên của chuỗi (n = 1) [16, 18]. Với tính chất trên, người ta thường dùng số
hạng đầu tiên của chuỗi (1) để biểu diễn mối quan hệ giữa giá trị trọng lực và
địa hình mặt ranh giới, khi đó ta có [2, 16, 18]:
![]() (2)
(2)
Công thức (2) cho phép ta xác định trực tiếp địa hình
mặt ranh giới phân chia mật độ thông qua giá trị dị thường trọng lực theo công
thức biến đổi ngược sau:
![]() (3)
(3)
trong đó: F
-1 là toán tử biến đổi Fourier ngược hai chiều.
Ưu điểm nổi bật của thuật toán này là chúng ta có thể xác định nhanh và
chính xác địa hình mặt ranh giới khi biết được độ tương phản mật độ và độ sâu
trung bình của mặt ranh giới. Phương pháp trên đã được Sandwell và Smith áp dụng
đặc biệt có hiệu quả trong việc xác định địa hình đáy biển toàn cầu từ số liệu
trọng lực vệ tinh [16, 18].
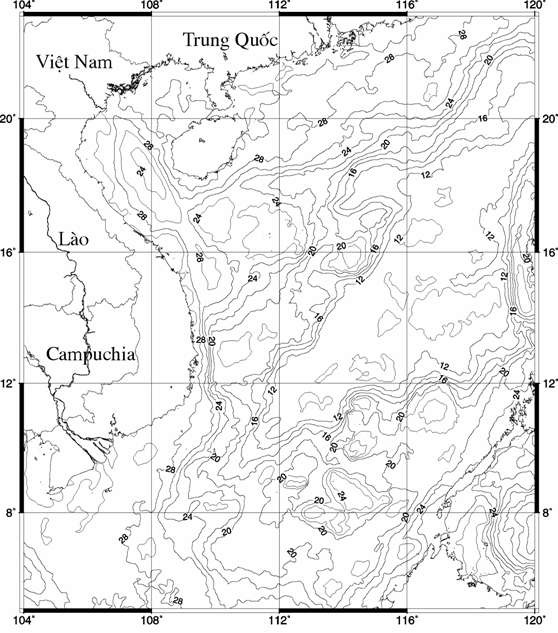
Hình 4a. Bản đồ độ sâu mặt Moho tính theo phương
trình hồi quy (4).
Thiết diện đường đồng mức 2 km
Để tính độ sâu mặt Moho
chúng tôi giả thiết vỏ Trái đất gồm 4 lớp: lớp nước biển, lớp trầm tích, lớp đá
móng và manti và tiến hành viết chương trình GRA3Dinv trên ngôn ngữ Fortran và
GMT theo lược đồ tính toán sau:
a) Tính hiệu ứng trọng lực
của lớp nước biển và địa hình mặt móng gây ra theo công thức (1);
b) Tính dị thường dư do mặt
Moho gây ra, hay dị thường manti Bouguer, bằng cách lấy dị thường Fai trừ đi
hiệu ứng trọng lực của lớp nước biển và địa hình mặt móng (xem hình 2b).
c) Tính địa hình mặt Moho
từ các dị thường dư theo công thức (3).
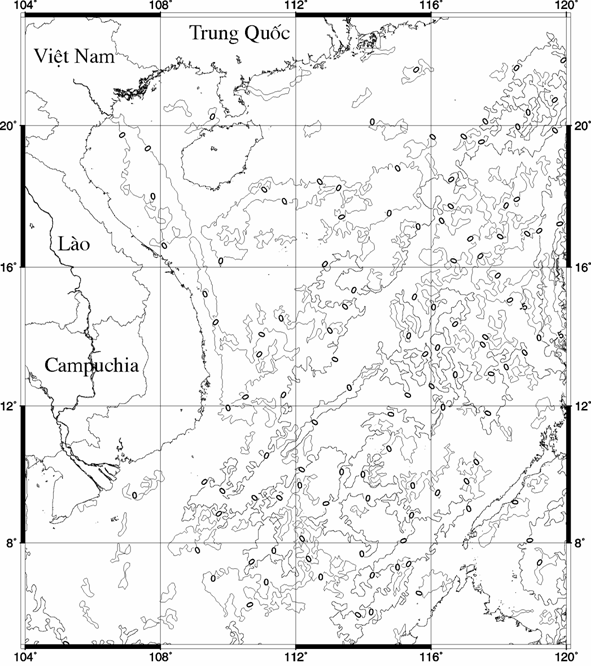
Hình 4b. Bản đồ độ lệch giữa mặt Moho tính theo
phương pháp bài toán ngược 3D
và phương pháp tương quan hồi quy (theo %). Thiết diện đường đồng mức 5%
Giá trị độ sâu mặt Moho
tính được theo thuật toán nêu trên có độ chính xác phụ thuộc rất nhiều vào việc
chọn giá trị độ sâu trung bình (d) của mặt Moho [12, 16]. Bằng cách lấy độ sâu
mặt Moho xác định theo địa chấn làm điểm khống chế nghiệm và chọn (d0)
ban đầu theo [11], sau một số lần tính
lặp chúng ta xác định được giá trị độ sâu trung bình mặt Moho tốt nhất (d).
Hình 3 là bản đồ độ sâu mặt Moho được tính toán và vẽ bằng chương trình
GRA3Dinv.bat
2. Phương pháp tương quan hồi quy
Độ sâu mặt Moho được
xác định trên cơ sở mối quan hệ tương quan giữa 42 điểm độ sâu mặt Moho xác định
bằng địa chấn sâu với dị thường trọng lực manti Bouguer [10]. Mối tương quan
(R2) này đạt đến –0.97, phương trình hồi
quy tuyến tính biểu diễn mối quan hệ giữa dị thường manti Bouguer và độ sâu mặt
Moho như sau [9]:
Y = -0.0576 * X + 28.4776 (4)
trong
đó: Y là độ sâu mặt Moho (Km); X là giá
trị dị thường manti Bouguer (mGal).
Hình 4a và 4b là bản đồ độ sâu mặt Moho hồi quy xác định theo phương trình
hồi quy (4) và bản đồ độ lệch so với bản đồ mặt Moho 3D.
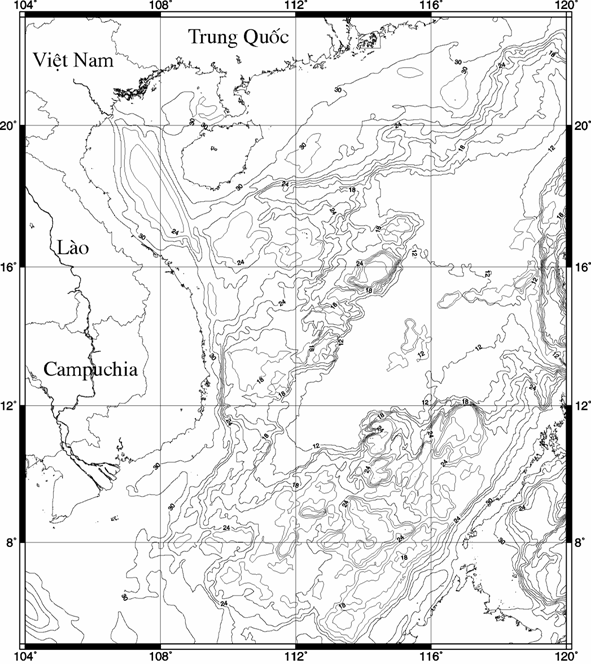
Hình 5a. Bản đồ độ sâu mặt Moho tính theo phương
pháp mô hình bù đẳng tĩnh.
Thiết diện đường đồng mức 5 km
3. Phương pháp mô hình bù đẳng tĩnh
Airy
Độ sâu mặt Moho có thể
được xác định trên cơ sở mô hình bù đẳng tĩnh của Airy [1]. Theo mô hình này, vỏ
Trái đất được giả thiết là nhẹ và nổi lên trên phần đá lỏng manti. Khi đó những
vùng vỏ Trái đất có địa hình phía trên nhô cao hoặc hạ thấp thì địa hình mặt
Moho phía dưới sẽ hạ thấp hoặc nhô cao theo nguyên lý sao cho tổng khối lượng
đất đá từ trên mặt địa hình đến một độ sâu nhất định là một giá trị không đổi [1]. Phương trình xác
định độ sâu mặt Moho đẳng tĩnh theo mô hình vỏ 4 lớp nêu ở phần trên có dạng sau
[10]:
![]() (5)
(5)
trong
đó: Hm, Hw và Hz là độ sâu mặt Moho cần
tính, độ sâu đã biết của địa hình đáy biển và địa hình mặt móng tại điểm cần tính. Hw0, Hz0 và Hm0 là độ sâu
đã biết của địa hình đáy biển, móng trầm tích và mặt Moho tại điểm tựa. Drm, Drbz, Drzw là độ tương phản mật độ giữa manti và đá
móng, đá móng và đá trầm tích, và giữa đá trầm tích và nước biển. Hình 5a và 5b
là bản đồ mặt Moho đẳng tĩnh tính được theo phương trình đẳng tĩnh (5) với các
tham số mật độ Drm, Drbz, Drzw là 0,4, 0,24 và 1,64 g/cm3
[11] và bản đồ độ lệch so với mặt Moho 3D.
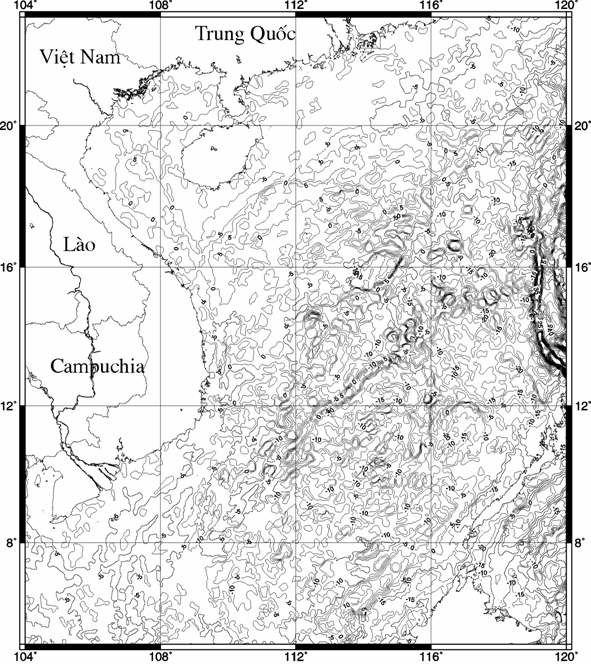
Hình 5b. Bản đồ độ lệch giữa mặt Moho tính theo
phương pháp bài toán ngược 3D
và phương pháp mô hình đẳng tĩnh (%). Thiết diện đường đồng mức là 5%
IV. ĐỐI SÁNH CÁC KẾT QUẢ TÍNH TOÁN
1. So sánh kết quả tính toán với số liệu
địa chấn: Các giá trị độ sâu mặt
Moho tính được theo ba phương pháp trên đem so sánh với giá trị độ sâu xác định
bằng địa chấn tại các điểm OBS, ESP và Sonobuoy [7,
11, 20, 21]. Kết quả cho thấy độ sâu mặt Moho
tính được theo ba cách trên đều có độ chính xác cao, trong đó kết quả tính theo
phương pháp bài toán ngược 3D và phương pháp tương quan hồi quy cho độ chính xác
cao nhất (5,5-5,9%) và kết quả tính theo phương pháp mô hình bù đẳng tĩnh đạt
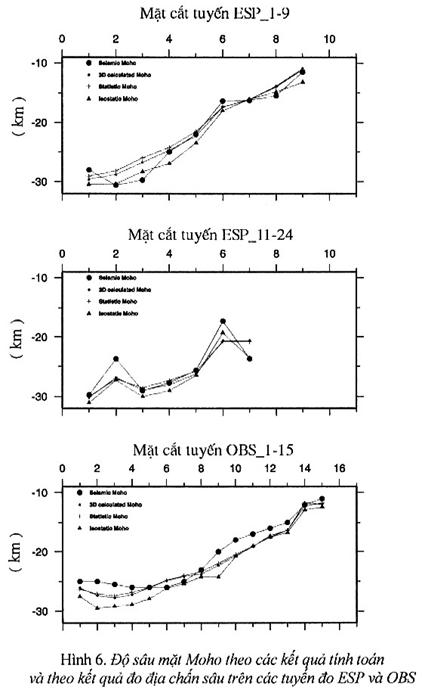
9,4 % (xem hình 6). Nếu xét độ chính xác của các kết quả tính theo các khu vực
thềm lục địa, sườn lục địa và bồn trũng Trung tâm chúng ta thấy (xem bảng 1):
đối với phương pháp tính giải bài toán ngược 3D và phương pháp tương quan hồi
quy thì ở khu vực thềm lục địa và trũng sâu biển Đông kết quả tính có độ chính
xác cao nhất (4,7-5,2%). Tại khu vực sườn lục địa độ chính xác thấp hơn, đạt 7,1
- 7,4%; đối với phương pháp tính theo mô hình đẳng tĩnh Airy thì ở khu vực trũng
sâu biển Đông kết quả tính có độ chính xác thấp nhất (13,4%). Tại khu vực thềm
và sườn lục địa kết quả tính có độ chính xác cao hơn (7,1 - 7,4 %).
Bảng 1. Độ chính xác của các kết quả tính toán theo
các vùng khác nhau trên biển Đông
|
STT |
Vùng khảo sát |
So sánh mặt Moho theo địa chấn
với các kết quả tính toán |
||
|
P/p bài toán ngược 3D (%) |
P/p tương quan hồi quy (%) |
P/p bù đẳng tĩnh
Airy (%) |
||
|
1 |
Vùng trũng sâu biển
Đông |
4,7 |
4,9 |
13,4 |
|
2 |
Vùng sườn lục địa |
7,4 |
7,1 |
7,4 |
|
3 |
Vùng thềm lục địa |
4,8 |
5,2 |
7,4 |
2. So sánh mặt Moho hồi quy với mặt Moho
3D (xem hình 4b): Kết quả so sánh các mặt Moho 3D với mặt Moho hồi quy trên toàn bộ vùng nghiên
cứu cho thấy mặt Moho tính theo hai phương pháp này có độ phù hợp rất cao. Độ
sai lệch giữa hai kết quả tính này chỉ biến đổi trong khoảng 0-2 %, trừ một số
ít điểm tại các nơi như rìa trục tách giãn, rìa trũng sâu biển Đông, quần đảo
Trường Sa có độ lệch lên đến 4%.
3. So sánh mặt Moho đẳng tĩnh với mặt
Moho 3D (xem hình 5b): So sánh mặt Moho đẳng tĩnh với mặt Moho 3D cho thấy ở hầu
hết phần thềm lục địa và rìa lục địa Việt Nam và Trung Quốc, độ sâu mặt Moho
đẳng tĩnh thường sai lệch với mặt Moho 3D nhỏ, khoảng 0-5%. Phần bồn trũng Trung
tâm và khu vực quần đảo Trường Sa và nam Hoàng Sa, mặt Moho đẳng tĩnh sâu hơn
mặt Moho 3D đến 10-15%, khu vực phía đông của bồn trũng Trung tâm, Maclessfield,
Reed Bank lên đến 20-25%. Ở phần trũng sâu
V. ĐẶC ĐIỂM ĐỊA HÌNH MẶT MOHO
Phần thềm lục địa và
sườn lục địa, độ sâu mặt Moho thay đổi từ 31 km đến 16 km,
càng về phía trũng sâu biển Đông địa hình mặt Moho càng nâng cao. Mặt Moho nâng
cao nhất ở phần bồn trũng Trung tâm với chiều sâu thay đổi trung bình từ 10 đến
12 km. Hình dạng các đường đẳng sâu, các vùng građien địa hình cao đặc biệt phù
hợp với các ranh giới vỏ đại dương – vỏ lục địa, các đới cấu trúc phá huỷ, cấu
trúc chạc ba Nam vịnh Bắc Bộ, các bồn trũng Kainozoi, các khối nâng Hoàng Sa,
Trường Sa... Đặc điểm cấu trúc của mặt Moho tại từng khu vực như sau (xem hình
3).
1. Khu vực vịnh Bắc Bộ: Ở
khu vực bồn trũng Sông Hồng, độ sâu mặt Moho thay đổi từ 30 km dọc theo đường bờ
đến 24 km ở phần trung tâm bồn trũng. Các đường đồng mức địa hình có dạng kéo
dài theo hướng TB-ĐN, hẹp và dốc theo hướng ĐB-TN. Ở phần trung tâm bồn trũng
Sông Hồng, địa hình mặt Moho nâng cao tạo thành cấu trúc dương chạy dọc theo
hướng TB-ĐN. Khu vực bồn trũng Lôi Châu nằm ngay phía đông bắc của bồn trũng
Sông Hồng, địa hình mặt Moho tương đối bằng phẳng, hơi nâng cao ở phần trung
tâm, chiều sâu thay đổi trong khoảng 28-30 km.
2. Khu vực Bắc Trung Bộ và quần đảo
Hoàng Sa: Độ sâu mặt Moho thay
đổi trong khoảng rộng 16-30 km. Dọc theo bờ biển và phần ngoài khơi, các đường
đồng mức địa hình định hướng dọc theo phương B-N, tại địa hào Quảng Ngãi, địa
hình mặt Moho nâng lên (26-27 km) và hạ thấp dọc theo đường bờ và địa luỹ Tri
Tôn (28-30 km). Khu vực quần đảo Hoàng Sa các đường đồng mức địa hình có cấu tạo
dạng vòm âm (lòng chảo). Ở phần trung tâm khối nâng Hoàng Sa, mặt Moho hạ thấp
(28 km), và nâng cao dần về các phía. Phần phía bắc của quần đảo Hoàng Sa ngăn
cách với phần thềm lục địa nam Trung Quốc bởi một dải các đường đồng mức (24-26
km) định hướng theo phương ĐB. Phía nam quần đảo Hoàng Sa cũng được giới hạn bởi
các đường đồng mức 16-20 km định hướng theo phương ĐB-TN.
3. Khu vực bồn trũng Phú Khánh: Độ sâu mặt Moho thay đổi mạnh từ 31-16 km. Phần phía tây của bồn trũng,
dọc theo thềm lục địa, mặt Moho chìm sâu xuống 31-26 km. Phần ngoài khơi địa
hình mặt Moho tương đối phẳng và nâng lên rất cao (18-16 km), tạo thành một địa
hình dạng bậc chạy theo hướng B-N và ĐB-TN.
4. Phần thềm lục địa
5. Rìa bắc biển Đông (Nam Trung Quốc): Giống như thềm lục địa Nam Việt Nam, thềm lục địa Nam Trung
quốc có địa hình mặt Moho tương đối thoải, nâng cao dần về phía biển. Chiều sâu
mặt Moho thay đổi từ 30 đến 22 km. Phần sườn và chân lục địa, địa hình mặt Moho
nâng cao (22-16 km). Các đường đồng mức địa hình có dạng dải theo phương ĐB-TN,
phần građien địa hình cao chủ yếu chạy dọc theo sườn lục địa.
6. Khu vực bồn trũng Trung tâm: Địa hình mặt Moho phản ánh rõ hình dạng của bồn trũng Trung
tâm. Tại đây, mặt Moho trồi hẳn lên so với xung quanh, hình thành một bình diện
tương đối phẳng cho toàn khu vực bồn trũng. Độ sâu đến mặt Moho trung bình
khoảng 10-11 km. Dọc theo trục giãn đáy địa hình mặt Moho hạ thấp tạo thành một
dải trũng có độ sâu khoảng 12-13 km. Phía bắc của bồn trũng, tính từ trục giãn
đáy, mặt Moho chìm sâu hơn phần phía nam. Dọc theo đới hút chìm
7. Rìa nam biển Đông (quần đảo Trường Sa
và lân cận): Địa hình mặt Moho biến
đổi gồ ghề phức tạp, tạo ra các đới nâng trồi hoặc sụt võng xen kẽ nhau. Tại các
khu vực khối nâng Đá Lát – Chữ Thập, Hoa Lau- Thám Hiểm, cụm đảo Trường Sa, Bãi
Sinh Tồn - Nam Yết và Cỏ Rong, mặt Moho chìm sâu đến 24-28 km. Khu vực trũng Nam
Yết, Tiên Nữ, Châu Viên và Palawan, mặt Moho nâng cao đến 18-20 km. Phần nam
Trường Sa và trũng Tư Chính – Vũng Mây, địa hình mặt Moho tương đối bằng phẳng,
độ sâu trung bình khoảng 20 km.
VI. TUỔI CỦA ĐỊA HÌNH MẶT MOHO
Có hai cách có thể sử
dụng để đánh giá nguồn gốc và tuổi của sự biến đổi địa hình mặt Moho: 1) so sánh
sự biến đổi của địa hình mặt Moho với địa hình trên mặt để kiểm tra xem những
biến đổi này có liên quan đến các chu kỳ nén ép hay tách giãn không; và 2) kiểm
tra xem những biến đổi của địa hình mặt Moho có phù hợp với các cấu trúc địa
chất đã biết tuổi. Sự so sánh giữa các đơn vị cấu trúc - kiến tạo với các đặc
điểm biến đổi địa hình mặt Moho cho thấy, hầu hết các biến đổi về địa hình mặt
Moho đều có dấu hiệu liên quan đến quá trình hình thành và tiến hoá của các đơn
vị cấu trúc kiến tạo trong Kainozoi:
-
Dọc theo đới trượt bằng đứt gãy
Sông Hồng và đứt gãy 1100: địa hình mặt Moho có dạng dải nhô, chạy
dọc theo đới này.
-
Dọc theo ranh giới vỏ đại dương –
vỏ lục địa: các đường địa hình dạng dải khép kín bao lấy khối vỏ đại dương.
-
Khối cấu trúc Maclesfield và Reed
Bank: các đường địa hình dạng dải bao quanh lấy hai đảo nổi này.
-
Khối cấu trúc Trường Sa và Hoàng
Sa: các đường địa hình dạng khối, bao quanh lấy các đảo nổi, khối nhô.
-
Các bồn trũng Cửu Long, Nam Côn
Sơn, Phú Khánh, Vịnh Bắc Bộ, bồn trũng Lôi Châu: các đường địa hình là các khối
nhô.
-
Dọc theo thung lũng trục tách giãn:
các đường địa hình dạng dải chạy dọc theo thung lũng tách giãn.
-
Dọc theo đới hút chìm
Trong đó, biến đổi địa
hình mặt Moho có tuổi trẻ nhất nằm dọc theo đới hút chìm
VII. TRẠNG THÁI CÂN BẰNG ĐẲNG TĨNH VỎ
Để xác định trạng thái
bù đẳng tĩnh của vỏ Trái đất, chúng ta xét mức độ võng xuống của vỏ Trái đất do
tải trọng của địa hình có bước sóng (l). Công thức xác định
biên độ võng của vỏ được viết như sau [21]:
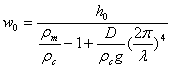 (6)
(6)
trong đó: w0 là độ võng xuống của vỏ Trái
đất; h0 - chiều cao của địa hình; rs – mật độ của vỏ; rm – mật độ manti; D - độ
cứng đàn hồi của vỏ; g – hằng số trọng lực.
Công thức trên cho thấy
vỏ Trái đất đạt trạng thái bù toàn phần (100%) khi tỷ số D/l đủ bé (khi địa hình có bước sóng đủ lớn hoặc độ cứng đàn
hồi của vỏ đủ nhỏ), nghĩa là công thức (6) trở về dạng công thức bù đẳng tĩnh
Airy:
wmax = hrs /(rm- rs)
(7)
Công thức xác định
trạng thái bù đẳng tĩnh của vỏ Trái đất (C) được tính bằng công thức sau [25]:
C = (w0/wmax
)100% (8)
Theo cách đánh giá
trên, ta có thể giả thiết giá trị mặt Moho 3D là mặt võng thực của vỏ Trái đất
(w0) và mặt Moho đẳng tĩnh là mặt Moho ở trạng thái bù 100% (wmax),
dựa vào kết quả này cho phép ta đánh giá được trạng thái bù đẳng tĩnh của vỏ
theo công thức (8). Trạng thái bù đẳng tĩnh của vỏ cũng được thể hiện qua giá
trị dị thường trọng lực. Tại những vùng vỏ có trạng thái bù đẳng tĩnh toàn phần
(C = 100%) thì giá trị dị thường trọng lực Fai dao động ở mức gần không, còn
những nơi trạng thái bù đẳng tĩnh càng thấp (C càng nhỏ) thì giá trị dị thường
trọng lực Fai càng cao [13]. Theo cách tính toán trên, trạng thái cân bằng đẳng tĩnh vỏ
tại khu vực biển Đông có thể được đánh giá như sau:
1. Rìa bắc, tây và tây nam biển Đông: Kết quả so sánh giữa mặt Moho 3D và mặt Moho đẳng tĩnh ở
phần trên cho thấy chúng có sự phù hợp rất cao ở phần rìa lục địa Việt
2. Rìa nam biển Đông: Ở khu vực quần đảo
Trường Sa, đảo nổi Maclesfield và Reed Bank, mặt Moho đẳng tĩnh thường nông hơn
mặt Moho 3D từ –10 đến -20%, tương ứng với trạng thái bù 80-90%. Sự sai khác này
chủ yếu tập trung dọc theo các khối nhô, đảo nổi. Như chúng ta biết, tại đây vỏ
lục địa đã bị biến dạng mạnh mẽ qua nhiều thời kỳ địa chất khác nhau, các hoạt
động núi lửa từ cổ đến trẻ xảy ra nhiều [8,
9, 21], đã
tạo ra địa hình đáy biển rất gồ ghề, nhấp nhô. Chúng tôi cho rằng trạng thái bù
đẳng tĩnh tại khu vực này đạt 80-90% chủ yếu là do yếu tố địa hình gây ra (địa
hình có bước sóng ngắn). Điều này cũng được thể hiện khá rõ trên dị thường trọng
lực Fai, tại đây giá trị dị thường Fai rất lớn, chúng hình thành nhiều khối dị
thường dương rất cao nằm trên nền dị thường khu vực cao. Tại khu vực trũng
Palawan, nằm phía nam quần đảo Trường Sa, mặt Moho đẳng tĩnh nông hơn mặt Moho
3D không nhiều (0 đến 10%), dị thường trọng lực Fai thay đổi trong khoảng +20
đến –40 mGal, có thể cho rằng trạng thái bù đẳng tĩnh đã được thiết lập ~100%.
Trạng thái đẳng tĩnh này có thể phù hợp với giả thiết đới hút chìm này đã
ngừng hoạt động vào trước Miocen. Khi đó mảng đại dương cắm xuống, dần dần dựng
đứng và tiêu biến đi [9,
19] và môi
trường dần dần trở về trạng thái cân bằng đẳng tĩnh hoàn toàn.
3. Khu vực trũng Trung tâm và đới hút
chìm
độ sâu mặt Moho 3D nhỏ
hơn giá trị độ sâu Moho đẳng tĩnh 10-20%, khu vực phụ bồn trũng Đông và Đông Bắc
lên đến 30%. Điều này cho thấy trạng thái bù đẳng tĩnh ở khu vực này trung bình
80-90%, khu vực phụ bồn trũng Đông thấp hơn 70%. Như chúng ta biết, bồn trũng
Trung tâm là một bồn trũng đại dương trẻ 32-15,5 tr.n. [3, 22]. Vỏ Trái đất ở khu vực này đang chìm dần
xuống dưới mảng Philippine, phần vỏ đại dương phía trước đới hút chìm sẽ bị uốn
cong lên do hiệu ứng đàn hồi của vỏ [22]. Hai dấu hiệu trên có thể thấy được qua dị
thường trọng lực Fai tại khu vực này: các dị thường trọng lực Fai lớn nằm trên
một phông chung khoảng 25-30 mGal, trong khi đó độ sâu của địa hình đáy biển > 4
km. Khu vực đới hút chìm Manila, mặt Moho 3D sâu hơn nhiều so với mặt Moho đẳng
tĩnh, sự sai khác này lên đến 50%. Sự sai khác này có thể giải thích như sau:
tại đây mảng vỏ đại dương đang cắm chìm dần dưới quần đảo Philippine, do mảng
đại dương đang trong quá trình cắm sâu xuống manti nên trạng thái bù đẳng tĩnh
chưa được thiết lập. Dấu hiệu này được thể hiện khá rõ trên dị thường Fai. Tại
đây giá trị dị thường âm rất nhỏ từ –100 đến -120 mGal. Hiệu ứng âm này chính là
do mặt Moho bị chìm sâu xuống gây ra, mà không được bù lại bằng sự nâng lên của
địa hình đáy biển (tại đây địa hình đáy biển rất sâu). Do đó, có thể nói rằng
trạng thái mất cân bằng đẳng tĩnh đang diễn ra tại đây.
KẾT LUẬN
Từ các kết quả phân
tích trên, chúng tôi có một số kết luận
sau:
Phương pháp giải ngược
trực tiếp 3D số liệu dị thường trọng lực để xác định độ sâu mặt Moho, với nghiệm
được khống chế bởi số liệu địa chấn sâu, đã cho kết quả có độ chính xác cao. Sai
số giữa kết quả tính toán so với số liệu địa chấn sâu đạt đến 5,6%, trong đó ở
khu vực thềm lục địa và trũng sâu biển Đông, kết quả tính có độ sai số nhỏ nhất.
Mặt Moho đẳng tĩnh có sai số lớn nhất so với mặt Moho địa chấn, đặc biệt tại khu
vực trũng sâu biển Đông lên đến 13,4%. Mặt Moho 3D, Moho hồi quy có sự phù hợp
cao cả về hình dạng và độ sâu trên cả ba vùng vỏ lục địa, vỏ đại dương và vỏ
chuyển tiếp. Dị thường trọng lực manti Bouguer và mặt Moho tại các khu vực khác
nhau trong vùng nghiên cứu đều có mối tương quan cao và có thể thoả mãn phương
trình (4).
Trạng thái cân bằng
đẳng tĩnh toàn phần phân bố chủ yếu trên phần rìa lục địa phía bắc, tây và tây
nam biển Đông. Phần rìa nam biển Đông và bồn trũng Trung tâm trạng thái bù đẳng
tĩnh đạt 80-90%. Trạng thái mất cân bằng đẳng tĩnh lớn nhất tập trung tại khu
vực đới hút chìm
Địa hình mặt Moho có
mối tương quan chặt chẽ với các đơn vị kiến tạo trong khu vực như bồn trũng
Trung tâm, đới hút chìm, đới đứt gãy trượt bằng, các bồn trũng Đệ tam...
Sự uốn lượn, biển đổi
của địa hình mặt Moho hình thành chủ yếu trong thời kỳ hoạt động của hệ
thống đứt gãy Sông Hồng, đứt gãy kinh tuyến 1100, quá trình tách giãn
mở biển Đông hình thành nên bồn trũng Trung tâm và các bồn trũng Đệ tam và quá
trình hút chìm của vùng vỏ đại dương xuống dưới mảng Philippine.
Lời cám ơn: Công trình này được
hoàn thành với sự trợ giúp của Chương trình Nghiên cứu cơ bản giai đoạn
2004-2005.
VĂN LIỆU
1. Airy G. B., 1855. On the computation of the effect of the attraction
of the mountain-masses, as disturbing the apparent astronomical latitude of
stations in geodetic surveys. Philos.
Trans. R. Soc., 145 : 101-104.
2. Blakely R. J., 1995. Potential theory in gravity and Magnetic
application.
3. Briais
A., Patrat P. & Tapponnier P., 1993. Updated interpretation of magnetic anomalies and reconstruction of the SCS
basin: implications for the Tertiary evolution of
4. Chen B. and Lei S., 1987. Free air anomalies. In Atlas of geology and geophysics of the
5. Feng Z., Miao W., Zheng W., Chen
W., 1992. Structure and hydrocarbon
potential of the para-passive continental margin of the
6. Hayes D.E., Nissen S.S., Buhl P.,
Diebold J., 1995. Throughgoing
crustal faults along the northern margin of the
7. Ludwig W.J.,
Kumar N., and Houtz R.E., 1979.
Profiler-sonobuoy measurement in the
8. Nguyễn Như Trung, Nguyễn Huy Hoàng,
Nguyễn Thị Thu Hương và Phạm Hồng Hải, 2002. Đặc trưng cấu trúc vùng quần đảo Trường Sa theo số liệu trọng lực vệ tinh.
TC Các Khoa học về Trái đất, 3.
9. Nguyễn Như Trung, Nguyễn Thi Thu
Hương, 2003. Cấu trúc vỏ Trái đất khu vực Biển Đông theo số liệu trọng lực vệ tinh và
địa chấn sâu. Hội nghị KHCN Viện Dầu khí
25 năm xây dựng và trưởng thành, tr. 336 – 356. Hà Nội.
10.
Nguyễn Nhu Trung, Sang-Mook Lee, Bui Cong Que, 2004. Satellite gravity anomalies and their correlation with the major tectonic
features in the
11. Nissen S. S & Hayes D. E.,
1995. Gravity, heat flow, and
seismic constraints on the processes of crustal extension: North margin of the
12. Parker R.L., 1972. The repeat calculation of potential anomalies. Geophys. J. Royal Astr. Soc., 31 : 447-455.
13. Philip K. and Frederick J.V.,
1996. Global Tectonics. Blackwell Sci., UK, p.333.
14. Pigott J.D., Ru Ke, 1994. Basin superposition on the the northern margin of
the
15. Roques D., Cl. Rangin and Ph.
Huchon, 1997. Geometry and sense of
motion along the
16. Sandwell D. T., Smith W. H.F.,
1999. Bathymetric estimation,
appear in satellite altrimetry and earth science. Acad. Press.
17. Sandwell D. T. and Smith W. H. F.,
1997. Marine gravity anomaly from
Geosat and ERS 1 satellite altimetry. J.
Geophys. Res., 102 : 10039-10054.
18. Smith W. H.F. and D. T. Sandwell,
1994. Bathymetric prediction from
dense satellite altimetry and sparse shipboard bathymetry. J. of Geophys. Res., 99/B11 : 21803-21824.
19. Taylor B. & Hayes D. E., 1983. Origin and history of the
20. Taylor B. & Hayes D. E., 1980. The tectonic evolution of the
21. Trần Lê Đông, Trần Văn Hồi, Phạm
Tất Đắc, Phạm Đình Hiếu. 2000. Cơ
chế hình thành kiểu bẫy chứa dầu trong các đá macma ở mỏ Bạch Hổ và Rồng. Hội nghị KHCN “Ngành Dầu khí trước thềm thế
kỷ 21”, 1 : 81-91. Hà Nội.
22. Turcotte L. and G. Shubert, 1982. Geodynamics Application of Continuum Physics to Geological Problem. John Wily and Sons, p. 450.
23. Yan
Pin, Zhou Di, Lui Zhaoshu, 2001. A crustal
structure profile across the northern
continental margin of the
24.
25. Zhou Siaozhong, Jang Shaoren,
1994. Tectonostratigraphic
interpretation and comparison of Reed Bank – Pearl River Mouth. Transct. Anthology of geol. and geophys.
study of Nansha islands and neighboring area, II. Science Press, pp 9-15.