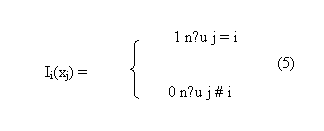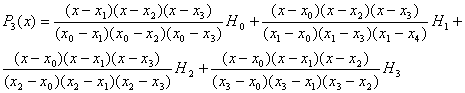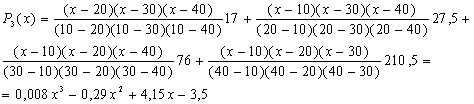SỬ
DỤNG ĐA THỨC LAGRANGE ĐỂ NỘI SUY TÀI LIỆU
QUAN TRẮC VÀ DỰ BÁO ĐỘNG THÁI NƯỚC DƯỚI ĐẤT
ĐẶNG
HỮU ƠN1, NGUYỄN CHÍ NGHĨA2
1Văn phòng Hội đồng Đánh giá TLKS, Trần
Hưng Đạo, Hà Nội
2Đại học Mỏ - Địa chất, Đông
Ngạc, Từ Liêm, Hà Nội
Tóm tắt: Đa thức Lagrange đã được sử dụng phổ biến rộng rãi để tìm mối quan hệ
giữa hàm và biến số từ các tài liệu thí nghiệm hoặc quan sát thực tế. Khi chỉnh
lý tài liệu quan trắc động thái rất cần phải xác định quy luật biến đổi của các
yếu tố động thái theo không gian và thời gian. Để giải quyết vấn đề này các tác giả đã sử dụng phép nội suy bằng
đa thức Lagrange trên cơ sở những số liệu thực nghiệm. Đa thức Lagrange
có dạng tổng quát như sau:
Pn(x)
= 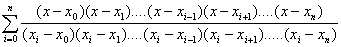
Sử dụng đa thức Lagrange có thể xác định
được hàm số biểu diễn quan hệ giữa mực nước và khoảng cách từ các lỗ khoan quan
sát đến sông. Từ kết quả nghiên cứu các tác giả đã rút ra kết luận:
- Khi chỉnh lý tài liệu quan trắc động
thái nước dưới đất (NDĐ), phương pháp nội suy Lagrange cho phép xác định quy
luật biến đổi của các yếu tố động thái (cao trình mực nước, lưu lượng, nhiệt
độ, thành phần hoá học của nước...) theo thời gian, không gian, cũng như theo
sự biến đổi của các nhân tố ảnh hưởng đến các yếu tố động thái.
- Kết hợp phương pháp nội suy Lagrange
với phương pháp thống kê cho phép ngoại suy khuynh hướng để dự báo sự phát
triển của động thái NDĐ theo thời gian và không gian.
I. ĐẶT VẤN ĐỀ
Tài
liệu quan trắc động thái nước dưới đất (NDĐ) là một trong những công cụ quản lý
tài nguyên nước, định hướng sử dụng hợp lý NDĐ và bảo vệ chúng. Quá
trình xử lý tài liệu thường cần xác định hàm số H = f(x), qua các giá trị quan
trắc được H0, H1….Hn ứng với các giá trị x0,
x1….xn trong khoảng xác định [a, b].
Thí dụ có một tuyến
quan trắc mực nước ngầm gồm 4 lỗ khoan (0, 1, 2,3) bố trí vuông góc với sông,
cách sông tương ứng - x0, x1, x2, x3,
tại một thời điểm đã quan trắc được cao
trình mực NDĐ ở các lỗ khoan - H0, H1, H2, H3,
yêu cầu xác định hàm H = f(x)? hay tại một lỗ khoan đã quan trắc được cao trình
mực nước H0, H1, H2, H3 ở các thời
điểm t0, t1, t2, t3, yêu cầu xác
định hàm H = f(t).
Các
yêu cầu nêu trên có thể được giải quyết khi sử dụng phép nội suy bằng đa thức
Lagrange [3].
II. THÀNH LẬP ĐA THỨC NỘI SUY LAGRANGE
Giả sử
có chuỗi quan trắc tại (x0, x1…. xn) biết (y0,
y1 … yn). Hãy tìm cách xây dựng đa
thức:
Pn(x) = a0xn + axn -
1 + … + an - 1x + an (1)
thoả mãn
điều kiện:
Pn(xi)
= f(xi) = yi ; i = 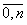 (2)
(2)
Ở đây: Pn(x)
- được gọi là đa thức nội suy của hàm f(x).
xi, i =
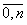 - các nút nội suy.
- các nút nội suy.
(a0, a...an) - giá
trị tham số xác định được khi thành lập hàm Lagrange.
Về mặt hình học có
nghĩa là tìm đường cong đi qua các điểm Mi(xi,
yi) đã biết (i = 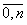 )
của đường cong y = j(x) (hình 1).
)
của đường cong y = j(x) (hình 1).
y = Pn(x) = a0xn + axn
– 1 + ….. + an – 1x + an
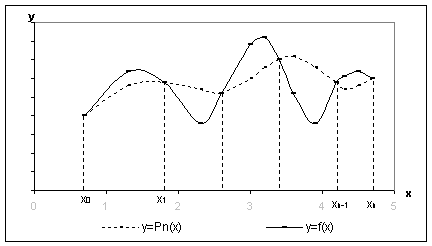
Hình 1. Đường
cong y = j(x)
Sau đó dùng đa thức Pn(x)
thay cho hàm số f(x) để tính gần đúng giá trị của hàm số f(x) tại các điểm x #
x1 (i = 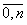 ).
Nếu điểm x
).
Nếu điểm x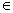 (x0,
xn) thì phép tính trên gọi là phép nội suy. Nếu x
(x0,
xn) thì phép tính trên gọi là phép nội suy. Nếu x 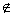 (x0,
xn) gọi là phép ngoại suy.
(x0,
xn) gọi là phép ngoại suy.
Cách
thành lập đa thức trên đã được trình bày trong các công trình [1, 2, 4].
Giả sử trên [a, b] cho
(n + 1) giá trị khác nhau của biến số: x0, x1 …. xn và biết những giá trị tương ứng của hàm số y =
f(x)
f(xi) = yi
; i = 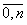 (3)
(3)
Lagrange đã xây dựng
đa thức nội suy Pn(x) thoả mãn điều kiện (4) như sau:
Pn(xi)
= yi ; i = 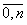 (4)
(4)
Trước hết xây dựng đa
thức Ii(x) thoả mãn điều kiện:
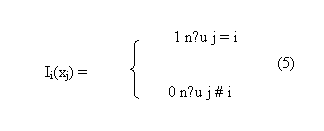
Vì đa thức Ii(x)
phải tìm triệt tiêu tại n điểm x0, x1 …. xi – 1 , xi + 1 …. xn, nên Ii(x) có thể viết dưới dạng :
Ii(x) = ci(xi
– x0) (xi – x1) …. (xi
– xi – 1)
(xi – xi + 1) …. (xi – xn) (6)
ở đây
ci là hằng số phải tìm.
Đặt x = xi
trong (6) và để ý đến điều kiện (5) ta có:
Ii(xi)
= ci(xi – x0) (xi – x1)
…. (xi – xi – 1) (xi – xi + 1) …. (xi
– xn)
(7)
Từ đó rút ra:
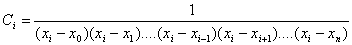 (8)
(8)
Thay (8) vào (6) ta được:
Ii(x) = 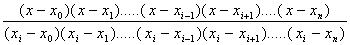 (9)
(9)
Đa
thức trên được gọi là đa thức Lagrange cơ bản.
Bây giờ ta xét đa thức
sau:
Pn(x) = 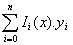 (10)
(10)
Bậc của đa thức Pn(x)
không cao hơn n và do điều kiện (5), ta có:
Pn(xj)=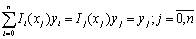 (11)
(11)
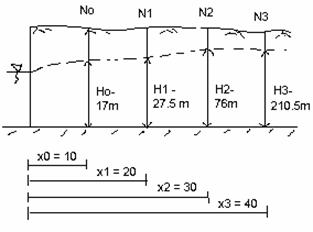
Hình
2. Tuyến các lỗ quan
trắc
Vậy
đa thức Pn(x), xác định bởi (10) là đa thức nội suy phải tìm. Thay
biểu thức Ii(x) từ (10) vào (11) nhận được:
Hình
2. Tuyến các lỗ khoan quan trắc
|
|
Pn(x) =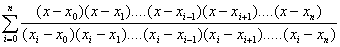 (12)
(12)
Đây
cũng là đa thức nội suy Lagrange.
Với n = 1, n = 2, đa
thức Lagrange có dạng:
P1(x) = 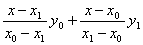 (13)
(13)
P2(x) = 
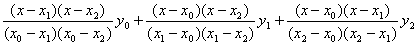 (14)
(14)
III.
VÍ DỤ NỘI SUY TÀI LIỆU QUAN TRẮC ĐỘNG THÁI NDĐ BẰNG ĐA THỨC LAGRANGE
Để
nghiên cứu động thái mực nước gần sông người ta đã thiết lập một tuyến các lỗ
khoan quan trắc vuông góc với sông (Hình 2).
Khoảng cách từ các lỗ khoan đến sông lần lượt là: x0 – 10 m, x1
– 20 m, x2 – 30 m, x3 – 40 m. Cao trình mực nước tại các
lỗ khoan vào một thời điểm nào đó như sau : H0 – 17 m, H1
– 27,5 m, H2 – 76 m, H3 – 210,5 m.
Hãy nội suy khuynh
hướng dâng cao mực nước bằng đa thức Lagrange và nội suy giá trị dâng cao tại x
= 25 m.
Ở đây n = 3 nên đa
thức nội suy là một đa thức bậc 3. Theo (12) ta có:
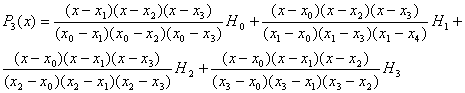
Thay số vào biểu thức
trên ta có:
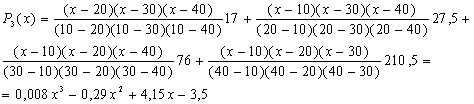
Với x = 25 m từ phương
trình trên tính được H = 44 m.
KẾT
LUẬN
Khi chỉnh lý tài liệu
quan trắc động thái NDĐ, phương pháp nội suy Lagrange cho phép xác định quy
luật biến đổi của các yếu tố động thái (cao trình mực nước, lưu lượng, nhiệt
độ, thành phần hoá học của nước...) theo thời gian, không gian, cũng như theo
sự biến đổi của các nhân tố ảnh hưởng đến các yếu tố động thái.
Kết hợp phương pháp
nội suy Lagrange với phương pháp thống kê cho phép ngoại suy khuynh hướng để dự
báo sự phát triển của động thái NDĐ theo thời gian và
không gian.
VĂN LIỆU
1. Dương Thuỷ Vỹ, 2002. Giáo trình
phương pháp tính. Nxb Khoa học và
Kỹ thuật, Hà Nội, tr. 92 - 111.
2. Nguyễn Chí Long, 2003. Phương
pháp tính. Nxb Đại học Quốc gia TP
Hồ Chí Minh, tr. 73 - 100.
3. Stengelov R.S. và nnk, 1994. Tính toán
thuỷ động lực trên máy tính điện tử. Nxb
MGU Moskva, tr. 7 - 79 (tiếng Nga).
4. Tạ Văn Đĩnh, 2003. Phương pháp tính.
Nxb Giáo dục, Hà Nội, tr. 66 - 77
![]()